题目内容
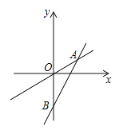
【题目】如图,一次函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求一次函数的表达式;
(2)求两直线与![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,若存在,直接写出
为腰的等腰三角形,若存在,直接写出![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)y=2x-5;(2)10;(3)存在,符合条件点C的坐标为(-5,0),(5,0)或(8,0).
【解析】
(1)由A点坐标可求得OA的长,由OA=OB则可求得B点坐标,代入可求得一次函数解析式;
(2)由A点坐标可求得OB边上的高,根据面积公式可求得△AOB的面积;
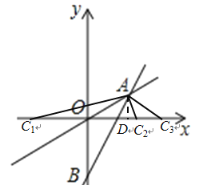
(3)分以下三种情况求解:①OA=OC且点C在x轴负半轴,如图点C1所示;②OA=OC且点C在x轴正半轴,如图点C2所示;③OA=AC,如图点C3所示.
解:(1)∵A(4,3),∴OA=5=OB,
∴B点坐标为(0,-5),
把A、B坐标代入y=kx+b可得![]() ,解得
,解得![]() ,
,
一次函数解析式为:y=2x-5;
(2)∵A(4,3),OB=5,
∴S△AOB=![]() ×4×5=10,
×4×5=10,
即两直线与y轴围成的三角形的面积为10;
(3)存在.理由如下:分以下三种情况求解:
①当OA=OC且点C在x轴负半轴时,如图点C1所示,
此时点C1的坐标为(-5,0);
②当OA=OC且点C在x轴正半轴,如图点C2所示,
此时点C2的坐标为(5,0);
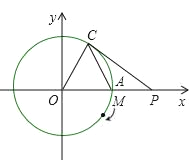
③当OA=AC时,如图点C3所示,
过点A作AD⊥x轴于点D,则有
OD=C3D=4,
∴OC3=8,
此时C3的坐标为(8,0).
综上所述,符合条件的点C的坐标为(-5,0),(5,0)或(8,0).

练习册系列答案
相关题目