题目内容
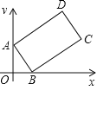
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93, ![]() ≈1.73)
≈1.73)
【答案】大约136米
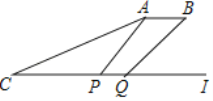
【解析】试题分析:根据三角形的外角的性质求得∠CAP的度数,证明△ACP是等腰三角形,则AP=CP=150米,作AE⊥CP,BF⊥CP分别于点E、F,在直角△APE中利用三角函数求得PE和AE的长,然后在直角△BQF中利用三角函数求得QF的长,根据CQ=CP+PQ=CP+PE+EF-QF即可求解.
试题解析:作AE⊥CP,BF⊥CP分别于点E. F.

∵∠APQ=∠C+∠CAP,
∴∠CAP=∠APQ∠ACP=60°30°=30°,
∴∠ACP=∠CAP,
∴AP=CP=150(米),
在直角△APE中,AE=APsin∠APE=150×3![]() =75
=75![]() (米),
(米),
PE=APcos∠APE=150×cos60°=75(米).
∵在直角△BQF中,BF=AE=75![]() 米.
米.
tan∠BQF=![]() ,
,
∴QF=BFtan∠BQF=![]() .
.
∴则CQ=CP+PQ
=CP+PE+EFQF
=150+75+50![]()
=150+125![]()
≈275![]() 75×1.730.93
75×1.730.93
≈275139.5
≈136(米)
答:伤员需前行136米才能够到云梯。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目