题目内容
【题目】如图,矩形ABCD中,AB=2,BC=4,点A、B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是 .
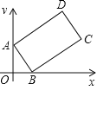
【答案】(1+2![]() ,2).
,2).
【解析】
试题分析:根据30°角所对的直角边等于斜边的一半求出OB的长度,然后过点C作CE⊥x轴于点E,根据直角三角形的性质求出∠CBE=30°,在Rt△BCE中求出CE、BE的长度,再求出OE的长度,即可得解.
试题解析:∵AB=2,∠OAB=30°,
∴OB=![]() AB=1,
AB=1,
在矩形ABCD中,∠ABC=90°,
∴∠OAB+∠ABO=90°,∠AB0+∠CBE=90°,
∴∠CBE=∠OAB=30°,
点C作CE⊥x轴于点E,
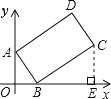
在Rt△BCE中,CE=![]() BC=
BC=![]() ×4=2,BE=
×4=2,BE=![]() ,
,
∴OE=OB+BE=1+2![]() ,
,
∴点C的坐标是(1+2![]() ,2).
,2).

练习册系列答案
相关题目
【题目】阅读下列信息;据报道,全世界受到威胁的动物种类数如下表所示.请你按照下面要求回答问题:
全世界受到威胁的动物种类数 | ||||
动物分类 | 哺乳类 | 鸟类 | 爬行类 | 两栖类 |
受到威胁的种类数(种) | 约1100 | 约1100 | 约300 | 约100 |
(1)制作适当的统计图表示表中的数据,你选择的统计图是____________________;
(2)通过学习本题,请你写一句20字左右的感想.
【题目】正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.