Question

【题目】如图所示，矩形ABCD的对角线相交于点O，OF⊥AD于点F，OF=2cm，AE⊥BD于点E，且BE﹕BD=1﹕4，求AC的长．

Answer 1

【答案】解法一：∵四边形ABCD为矩形， ∴∠BAD=90°，OB=OD，AC=BD，
又∵OF⊥AD，
∴OF∥AB，
又∵OB=OD，
∴AB=2OF=4cm，
∵BE：BD=1：4，
∴BE：ED=1：3，
设BE=x，ED=3 x，则BD=4 x，
∵AE⊥BD于点E
∴AE2=AB2﹣BE2=AD2﹣ED2 ，
∴16﹣x2=AD2﹣9x2 ，
又∵AD2=BD2﹣AB2=16 x2﹣16，
∴16﹣x2=16 x2﹣16﹣9x2 ， 8 x2=32
∴x2=4，
∴x=2，
∴BD=2×4=8（cm），
∴AC=8 cm．
解法二：在矩形ABCD中，BO=OD= BD，
∵BE：BD=1：4，
∴BE：BO=1：2，即E是BO的中点，
又AE⊥BO，
∴AB=AO，
由矩形的对角线互相平分且相等，
∴AO=BO，
∴△ABO是正三角形，
∴∠BAO=60°，
∴∠OAD=90°﹣60°=30°，
在Rt△AOF中，AO=2OF=4，
∴AC=2AO=8．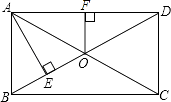

【解析】解法一：利用构建方程组的思想解决问题． 解法二：首先证明△ABO是正三角形，在Rt△AOF中，AO=2OF=4，由此即可解决问题．
【考点精析】根据题目的已知条件，利用矩形的性质的相关知识可以得到问题的答案，需要掌握矩形的四个角都是直角，矩形的对角线相等．