题目内容

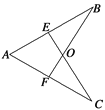
【题目】如图，AE＝AF，AB＝AC，EC与BF交于点O，∠A＝60°，∠B＝25°，求∠EOB的度数．

【答案】∠EOB＝70°.

【解析】

利用SAS可证明△ABF≌△ACE，根据全等三角形的对应角相等可得∠B=∠C，根据三角形外角的性质得到∠BFC=∠A+∠B，求出∠BFC的度数，在△FOC中，根据三角形的内角和定理求出∠COF的度数，最后根据对顶角相等可得∠EOB的度数．

在△ABF和△ACE中，

∵AF＝AE，∠A＝∠A，AB＝AC，

∴△ABF≌△ACE(SAS)．

∴∠B＝∠C.

∵∠B＝25°，∴∠C＝25°.

又∵∠CFB是△AFB的外角，∠A＝60°，

∴∠CFB＝60°＋25°＝85°，

∴∠COF＝180°－∠CFB－∠C＝180°－85°－25°＝70°.

又∵∠EOB＝∠COF，∴∠EOB＝70°.

练习册系列答案
相关题目

【题目】如图，△ABC中，∠A=65°，∠B=75°，将△ABC沿EF对折，使C点与C′点重合．当∠1=45°时，∠2=________°．

【题目】如图①，在平面直角坐标系中，抛物线y=x2﹣2mx+m2+m的顶点为A，与y轴交于点B．当抛物线不经过坐标原点时，分别作点A、B关于原点的对称点C、D，连结AB、BC、CD、DA．

（1）分别用含有m的代数式表示点A、B的坐标．

（2）判断点B能否落在y轴负半轴上，并说明理由．

（3）连结AC，设l=AC+BD，求l与m之间的函数关系式．

（4）过点A作y轴的垂线，交y轴于点P，以AP为边作正方形APMN，MN在AP上方，如图②，当正方形APMN与四边形ABCD重叠部分图形为四边形时，直接写出m的取值范围．

【题目】如图1，矩形ABCD中，AB=6，∠DBC=30°，DM平分∠BDC交BC于M，△EFG中，∠F=90°，GF= ，∠E=30°，点F、G、B、C共线，且G、B重合，△EFG沿折线B﹣M﹣D方向以每秒 个单位长度平移，得到△E1F1G1 ， 平移过程中，点G1始终在折线B﹣M﹣D上，△E1F1G1与△DBM无重叠时，△E1F1G1停止运动，设△E1F1G1与△DBM重叠部分面积为S，平移时间为t，

（1）当△E1F1G1的顶点G1恰好在BD上时，t=秒；
（2）直接写出S与t的函数关系式，及自变量t的取值范围；
（3）如图2，△E1F1G1平移到G1与M重合时，将△E1F1G1绕点M旋转α°（0°＜α＜180°）得到△E2F2G1 ， 点E1、F1分别对应E2、F2 ， 设直线F2E2与直线DM交于P，与直线DC交于Q，是否存在这样的α，使△DPQ为直角三角形？若存在，求α的度数和DQ的长；若不存在，请说明理由．

【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．

（1）求∠CAD的度数；

（2）延长AC至E，使CE=AC，求证：DA=DE．

【题目】如图，抛物线 与x轴相交于点A、B，与y轴相交于点C，抛物线对称轴与x轴相交于点M，

（1）求△ABC的面积；
（2）若p是x轴上方的抛物线上的一个动点，求点P到直线BC的距离的最大值；
（3）若点P在抛物线上运动（点P异于点A），当∠PCB=∠BCA时，求直线PC的解析式．

【题目】如图，E是矩形ABCD的边CB的中点，AF⊥DE于点F，AB=3，AD=4．求点A到直线DE的距离．

【题目】如图，在矩形ABCD中，已知AD＞AB，在边AD上取点E，连结CE，过点E作EF⊥CE，与边AB的延长线交于点F．
（1）证明：△AEF∽△DCE．
（2）若AB=2，AE=3，AD=7，求线段AF的长．

【题目】如图，P是正三角形ABC内的一点，且PA=6，PB=8，PC=10，将△APB绕点B逆时针旋转一定角度后，可得到△CQB．
（1）求点P与点Q之间的距离；
（2）求∠APB的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网