题目内容
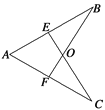
【题目】如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF= ![]() ,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒
,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒 ![]() 个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
(1)当△E1F1G1的顶点G1恰好在BD上时,t=秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0°<α<180°)得到△E2F2G1 , 点E1、F1分别对应E2、F2 , 设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由.
【答案】
(1)3
(2)
解:在Rt△DCM中,∵∠C=90°,CD=6,∠CDM=30°,
∴CM=2 ![]() ,DM=4
,DM=4 ![]() ,
,
∴BM=4 ![]() .
.
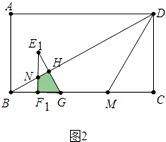
①如图2中,当0<t≤4时,重叠部分是四边形NF1GH,
S=S ![]() ﹣S
﹣S ![]() =
= ![]() ×3×
×3× ![]() ﹣
﹣ ![]() (2
(2 ![]() ﹣
﹣ ![]() t)(2﹣
t)(2﹣ ![]() t)=﹣
t)=﹣ ![]() t2+2
t2+2 ![]() t﹣
t﹣ ![]()
![]() ,
,
②如图3中,当4<t≤7时,重叠部分是四边形GHNF1,

S=S ![]() ﹣S
﹣S ![]() =
= ![]() ﹣
﹣ ![]() [2
[2 ![]() ﹣
﹣ ![]() (8
(8 ![]() ﹣
﹣ ![]() t)][2﹣
t)][2﹣ ![]()
![]() t2+
t2+ ![]() t﹣
t﹣ ![]() ,
,
③如图4中,当7<t≤8时,重叠部分是△GHN,

S= ![]()
![]() (8
(8 ![]() ﹣
﹣ ![]() t)
t) ![]() (8
(8 ![]() ﹣
﹣ ![]() t)=
t)= ![]() t2﹣6
t2﹣6 ![]() t+24
t+24 ![]() ,
,
综上所述,S= 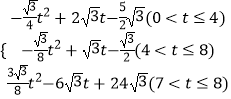
(3)
解:存在.
理由:①如图5中,当∠DQP=90°时,
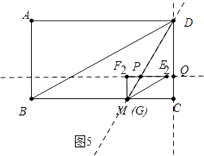
∵∠QCM=∠CQF2=∠QF2M=90°,
∴四边形MCQF2是矩形,
∴CQ=MF2= ![]() ,∠F2MC=90°
,∠F2MC=90°
∴α=90°,DQ=CD﹣CQ=6= ![]() .
.
②如图6中,当∠DPQ=90°时,点P与点F2重合,点E、Q、C重合,此时α=120°,DQ=CD=6.
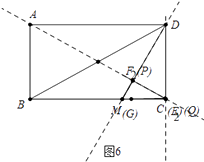
综上所述,当α=90°,DQ=6﹣ ![]() 或α=120°,DQ=6时,△DPQ为直角三角形
或α=120°,DQ=6时,△DPQ为直角三角形
【解析】解:(1)如图1中,连接AC交BD于点O,作OH⊥BC于点H.
∵四边形ABCD是矩形,
∴AB=CD=6,BO=OD,
∴BH=HC,
∴OH= ![]() CD=3,
CD=3,
在Rt△DBC中,∵CD=6,∠DBC=30°,
∴BC=6 ![]() ,BD=12,BH=HC=3
,BD=12,BH=HC=3 ![]()
∵在△EFG中,∠F=90°,GF= ![]() ,∠E=30°,
,∠E=30°,
∴EF=3,EB=2 ![]() ,
,
∴当△E1F1G1的顶点E1恰好在BD上时,点E平移到点O处.
此时t= ![]() =3,
=3,
∴t=3时,△E1F1G1的顶点E1恰好在BD上,
所以答案是3.
【考点精析】关于本题考查的翻折变换(折叠问题),需要了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案