题目内容
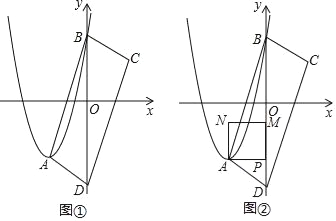
【题目】如图①，在平面直角坐标系中，抛物线y=x2﹣2mx+m2+
m的顶点为A，与y轴交于点B．当抛物线不经过坐标原点时，分别作点A、B关于原点的对称点C、D，连结AB、BC、CD、DA．
（1）分别用含有m的代数式表示点A、B的坐标．
（2）判断点B能否落在y轴负半轴上，并说明理由．
（3）连结AC，设l=AC+BD，求l与m之间的函数关系式．
（4）过点A作y轴的垂线，交y轴于点P，以AP为边作正方形APMN，MN在AP上方，如图②，当正方形APMN与四边形ABCD重叠部分图形为四边形时，直接写出m的取值范围．
【答案】（1）A（m， 
m），（0，m2+
m）；（2）点B能落在y轴负半轴上；（3）l=2m2﹣
m；（4）m＜﹣1．
【解析】试题分析：
（1）①把
配方化为顶点式，可得顶点A的坐标；②在
中，由
可得
，由此可得点B的坐标；
（2）由顶点A的位置可得“
”；由点B的坐标为
可知，若点B在
轴负半轴，则有
，两者结合可解得： 
时，点B就在
轴负半轴；
（3）由题意可知： 
=AC+BD=2OA+OB，由点A、B的坐标可用和含“
”的代数式表达出OA、OB的长度，从而可得
与
间的函数关系式；
（4）由题意可知，当AP<BP时，正方形APMN与四边形ABCD重叠部分图形为四边形时，由AP= 
，BP= 
列出不等式，结合
即可求出
的取值范围；
试题解析：
（1）∵把
配方，得： 
，
∴顶点A的坐标为
；
∵在
中，当
时， 
；
∴点B的坐标为
；
（2）点B能落在y轴负半轴上，理由如下：
由图可知顶点A
在第三象限，
∴
，
∵B点的纵坐标要小于零，
∴
，
由
，得： 
，
解得： 
，
即当
时，点B能落在
轴的负半轴上；
（3）由点A、B关于原点的对称点分别为C、D，可得：AC=2OA，BD=2OB，
∵A的坐标为
，B的坐标为
，
∴OA= 
，OB= 
，
∴
=AC+BD=2OA+2OB= 
；
（4）由题意，当正方形APMN与四边形ABCD重叠部分图形为四边形时，AP＜BP，
∵AP= 
，BP= 
，
∴
，即
，
又∵
，
∴
，解得： 
，
∴当正方形APMN与四边形ABCD重叠部分图形为四边形时， 
的取值范围是： 
.
