题目内容
【题目】如图，抛物线 
与x轴相交于点A、B，与y轴相交于点C，抛物线对称轴与x轴相交于点M，
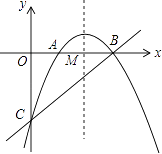
（1）求△ABC的面积；
（2）若p是x轴上方的抛物线上的一个动点，求点P到直线BC的距离的最大值；
（3）若点P在抛物线上运动（点P异于点A），当∠PCB=∠BCA时，求直线PC的解析式．
【答案】
（1）
解：令y=0，则有﹣ 
x2+4x﹣6=﹣ （x﹣2）（x﹣6）=0，
解得：x1=2，x2=6，
即点A（2，0），点B（6，0）．
令x=0，则y=﹣6，
即点C（0，6）．
∴AB=4，CO=6．
△ABC的面积S△ABC= ABCO= ×4×6=12
（2）
解：设直线BC的解析式为y=kx+b，
∵点B（6，0），点C（0，﹣6），
∴有 
，解得 
，
∴直线BC的解析式为y=x﹣6．
设经过动点P且平行于直线BC的直线解析式为y1=x+a．
将y1=x+a代入抛物线y=﹣ x2+4x﹣6中得： x2﹣3x+6+a=0，
若直线y1=x+a与抛物线相切，则有：
△=（﹣3）2﹣4× ×（6+a）=0，即3+2a=0，
解得：a=﹣ 
．
∴ 
﹣3x+6﹣ =0，即x2﹣6x+9=0，
解得：x=3，
将x=3代入y1=x﹣ ，得y1= ，
∴此时P点坐标为（3， ）在x轴上方．
∵直线BC的解析式为x﹣y﹣6=0，
∴点P到直线BC的距离= 
= 
．
故点P到直线BC的距离的最大值为
（3）
解：过点A作AE⊥BC与点E，并延长AE交直线CP与点D，如图所示．
∵点A（2，0），点B（6，0），点O（0，0），点C（0，﹣6），
∴AB=4，OA=2，OC=6，OB=6．
由勾股定理可知：AC= 
=2 
，BC= 
=6 
，
∴sin∠OBC= 
= 
= 
，AE=2 ．
∵∠PCB=∠ACB，且BC⊥AD，
∴CD=CA=2 ，DE=AE=2 （等腰三角形三线合一），
∴AD=AE+DE=4 ．
设点D坐标为（m，n），
则由两点间的距离公式可知，
，解得 
（舍去）或 
．
即此时点D的坐标为（6，﹣4）．
设直线CP的解析式为y=k1x﹣6，将D点坐标代入得：
﹣4=6k1﹣6，解得：k1= 
．
∴若点P在抛物线上运动（点P异于点A），当∠PCB=∠BCA时，直线PC的解析式为y= x﹣6．
【解析】（1）令x=0，可得点C坐标，令y=0，可得点A、B坐标，再结合三角形面积公式，即可得出结论；（2）找与直线BC平行且过动点P的直线，令此直线与抛物线相切，看切点P是否在x轴上方，如果在，则切点P到直线BC的距离就是所求最大距离，若不在，只需考虑端点A、B到直线BC的距离即可；（3）过点A作AE⊥BC与点E，并延长AE交直线CP与点D，巧妙利用等腰三角形的三线合一，找出AD、CD的长度，根据两点间的距离公式即可得出结论，不过此处要注意到会产生增根．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．
