Question

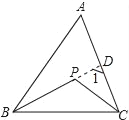
【题目】如图，已知：点P是内一点．

求证：；

若PB平分，PC平分，，求的度数．

Answer 1

【答案】（1）证明见解析（2）110°

【解析】

（1）根据三角形的一个外角大于和它不相邻的任何一个内角证明；

（2）根据三角形内角和定理可得∠ABC+∠ACB=140°，再由角平分线的定义结合三角形内角和定理即可求得∠P的度数.

（1）延长BP交AC于D，如图所示：

∵∠BPC是△CDP的一个外角，∠1是△ABD的一个外角，

∴∠BPC＞∠1，∠1＞∠A，

∴∠BPC＞∠A；

（2）在△ABC中，∵∠A=40°，

∴∠ABC+∠ACB=180°﹣∠A=180°﹣40°=140°，

∵PB平分∠ABC，PC平分∠ACB，

∴∠PBC=∠ABC，∠PCB=∠ACB，

在△PBC中，∠P=180°﹣（∠PBC+∠PCB）=180°﹣（∠ABC+∠ACB）

=180°﹣（∠ABC+∠ACB）=180°﹣×140°=110°．