Question

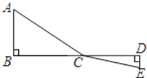
【题目】如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC. 已知AB=2，DE=1，BD=8，设CD=x.

(1)用含x的代数式表示AC+CE的长；

(2)求AC+CE的值最小；

(3)根据(2)中的规律和结论,请构图求出代数式的最小值。

Answer 1

【答案】(1) ；(2) 当A、C、E三点共线时，AC+CE的值最小，最小值为；(3)13.

【解析】

（1）由于△ABC和△CDE都是直角三角形，故AC，CE可由勾股定理求得；
（2）若点C不在AE的连线上，根据三角形中任意两边之和＞第三边知，AC+CE＞AE，故当A、C、E三点共线时，AC+CE的值最小；
（3）由（1）（2）的结果可作BD=12，过点B作AB⊥BD，过点D作ED⊥BD，使AB=2，ED=3，连接AE交BD于点C，则AE的长即为代数式的最小值，然后构造矩形AFDB，Rt△AFE，利用直角三角形的性质可求得AE的值．

解：（1）由线段的和差，得
BC=（8-x）．
由勾股定理，得
AC+CE== ；
（2）当A、C、E三点共线时，AC+CE的值最小，如图：作EF⊥AB于F点．，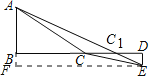
，
四边形BDEF是矩形，
BF=DE=1，EF=BD=8，
AF=AB+BF=2+1=3，
AE== =，

∴最小值为；

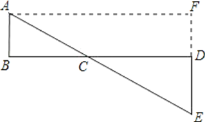
（3）如下图所示，作BD=12，过点B作AB⊥BD，过点D作ED⊥BD，使AB=2，ED=3，连接AE交BD于点C，设BC=x，则AE的长即为代数式的最小值．
过点A作AF⊥DE交ED的延长线于点F，得矩形ABDF，
则AB=DF=2，AF=BD=12，EF=ED+DF=3+2=5，
所以AE===13，
即的最小值为13．

故答案为：(1) ；(2) 当A、C、E三点共线时，AC+CE的值最小，最小值为；(3)13.