题目内容
【题目】已知A（8，0）及在第一象限的动点P（x，y），且x+y=10，设△OPA的面积为S
（1）求S关于x的函数表达式；
（2）求x的取值范围；
（3）求S=12时P点坐标；
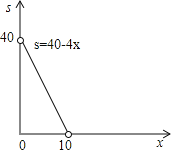
（4）画出函数S的图象．
【答案】（1）s=40﹣4x，（2）0＜x＜10，（3）P点坐标（7，3），（4）见解析
【解析】
试题分析：（1）首先把x+y=10，变形成y=10﹣x，再利用三角形的面积求法：底×高÷2=S，可以得到S关于x的函数表达式；
（2）P在第一象限，故x＞0，再利用三角形的面积S＞0，可得到x的取值范围；
（3）把S=12代入函数解析式即可；
（4）根据题意画出图象，注意x，y的范围．
解：（1）∵x+y=10
∴y=10﹣x，
∴s=8（10﹣x）÷2=40﹣4x，
（2）∵40﹣4x＞0，
∴x＜10，
∴0＜x＜10，
（3）∵s=12，
∴12=40﹣4x，
x=7
∴y=10﹣7=3，
∴s=12时，P点坐标（7，3），
（4）函数S的图形如图所示．
练习册系列答案
相关题目
【题目】下表是今年某水库一周内的水位变化情况(正号表示水位比前一天上升，负号表示水位比前一天下降)，该水库的警戒水位是
. (上周末的水位达到警戒水位).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/ |
|
|
|
|
|
|
|
(1)本周星期________河流的水位最高，水位是________
，本周星期________河流的水位最低，水位是________；
(2)本周三的水位位于警戒水位之_____(填“上”或“下”)，与警戒水位的距离是______；
(3)与上周末相比，本周末河流水位是上升了还是下降了？变化了多少米？
