题目内容
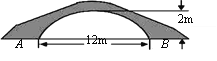
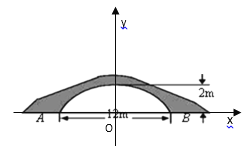
【题目】图示为一座拱桥,当水面宽AB为12m时,桥洞顶部离水面的距离为2m.
(1)若图中的拱形呈抛物线形状,当水面下降1m后,水面宽为多少?
(2)若图中的拱形呈圆弧形状,当水面下降1m后,水面宽又为多少?
【答案】(1)![]() m;(2)当水面下降1m后,水面宽为
m;(2)当水面下降1m后,水面宽为![]() m
m
【解析】
(1)先建立直角坐标系,求出函数解析式,计算当y=-1时的横坐标即可得到答案;
(2)设弧AB的圆心为O,过点O作AB的垂线,交弧于点D,垂足为点C,连接OB,设圆的半径为x m,根据勾股定理列方程求出半径,设水位下降1m后的水面宽为EF,交OD于点M,根据勾股定理即可求出答案.
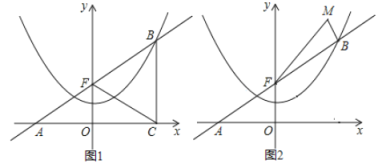
(1)以AB的中垂线为y轴建立直角坐标系,则点B(6,0),A(-6,0),
∵(0,2)在抛物线上,
∴设其抛物线为:y=ax2+2,
把(6,0)代入得:
0=a×62+2,
∴![]() ,
,
∴抛物线为:![]()
当y=-1时,
有![]() ,
,
解得![]() ,
,
∴此时水面的宽为:![]() (m);
(m);
(2)如图,设弧AB的圆心为O,过点O作AB的垂线,交弧于点D,垂足为点C,连接OB,
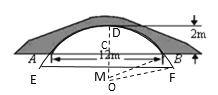
则CD=2,BC=6.
设圆的半径为x m,
则OC=(x-2)m
由勾股定理得:(x-2)2+62=x2
解得:x=10
设水位下降1m后的水面宽为EF,交OD于点M,则OM=10-3=7(m),
连接OF,由勾股定理得:
![]() m.
m.
∴当水面下降1m后,水面宽为![]() m.
m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目