题目内容
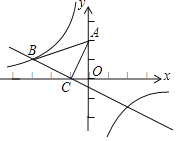
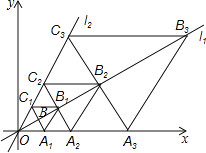
【题目】如图，在平面直角坐标系中，直线
：
，直线
，在直线上取一点
，使
，以点为对称中心，作点
的对称点
，过点作
∥
，交
轴于点
，作
∥轴，交直线于点
，得到四边形
；再以点为对称中心，作点的对称点
，过点作 
∥，交轴于点
，作
∥轴，交直线于点
，得到四边形
；…；按此规律作下去，则四边形
的面积是___________．
【答案】
【解析】
根据直线的解析式求得直线和
轴的夹角的大小，再根据题意求得
的长，然后依据直角三角形三角函数的求法求得
的长，进而求得
的长，然后根据等边三角形的性质，求得
，最后根据菱形的面积等于对角线积的一半即可求得．
解：
直线
，
直线
，
直线
与轴夹角为
，
直线
与轴夹角为
，
为上一点，且
，
根据题意可知：
，
，
，
，
，
，
四边形
、四边形
、四边形
是菱形，
，
△
，△
，
，△
，△
是等边三角形，
，
，
，
，
，
，
四边形
的面积
．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
