题目内容
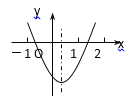
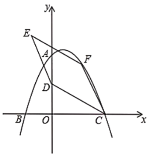
【题目】如图1,△ABC和△DEC均为等腰三角形,且∠ACB=∠DCE=90°,连接BE,AD,两条线段所在的直线交于点P.
(1)线段BE与AD有何数量关系和位置关系,请说明理由.
(2)若已知BC=12,DC=5,△DEC绕点C顺时针旋转,
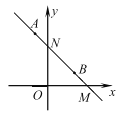
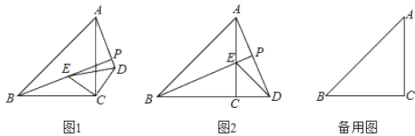
①如图2,当点D恰好落在BC的延长线上时,求AP的长;
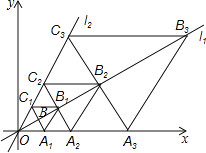
②在旋转一周的过程中,设△PAB的面积为S,求S的最值.
【答案】(1)BE=AD,BE与AD互相垂直,证明详见解析;(2)①AP=![]() ;②最小47,最大72
;②最小47,最大72
【解析】
(1)由题意根据等腰三角形的性质以及全等三角形的判定与性质,进行分析与等量代换即可;
(2)①由题意根据解直角三角形的勾股定理以及相似三角形的判定与性质进行分析即可;
②由∠APB=90°可知点P在以AB为直径的圆的一段弧上,且当BP与以CE为半径⊙C相切时,点P在其运动路径所在弧的两个端点处,P到AB的距离最小,此时△PAB的面积S最小;当点P与点C重合时,P到AB的距离最大,此时△PAB的面积S最大.
解:(1)BE=AD,BE与AD互相垂直;
证明:∵等腰△ABC,等腰Rt△DEC,
∴AC=BC,DC=EC,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE,
∴BE=AD,∠CAD=∠CBE,
∵∠CAD+∠APB=∠CBE+∠ACB=∠AOB,
∴∠APB=∠ACB=90°,即BE与AD互相垂直.
(2)①∵AB=BC=12,DC=EC=5,
∴AE=AC-EC=12-5=7,
Rt△BCE中,BE=![]() ,
,
由(1)同理可知∠APB=∠ACB=90°,∠CAD=∠CBE,
∴△APE∽△BCE,
∴![]() ,即
,即![]() ,解得AP=
,解得AP=![]() .
.
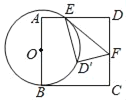
②由∠APB=90°可知点P在以AB为直径的圆的一段弧上,且当BP与以CE为半径⊙C相切时,点P在其运动路径所在弧的两个端点处,P到AB的距离最小,此时△PAB的面积S最小。如图1、2,易知四边形PDCE是边长为5的正方形.
∴ BE=AD=![]() ,BP=BE+PE=
,BP=BE+PE=![]() ,AP=AD-PD=
,AP=AD-PD=![]() ,
,
∴S(最小值)=![]() ×AP×BP=
×AP×BP=![]() ,
,
当点P与点C重合时,P到AB的距离最大,此时△PAB的面积S最大,如图3
S(最大值)=![]() ×AC×BC=
×AC×BC=![]() ×12×12=72.
×12×12=72.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?