Question

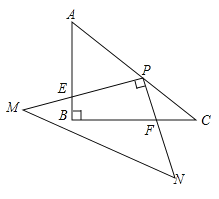
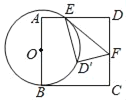
【题目】如图，D、E是以AB为直径的圆O上两点，且∠AED=45°，过点D作DC∥AB．

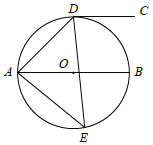
（1）请判断直线CD与圆O的位置关系，并说明理由；

（2）若圆O的半径为，，求AE的长；

（3）过点D作，垂足为F，直接写出线段AE、BE、DF之间的数量关系 ．

Answer 1

【答案】（1）相切，理由见解析；（2）12；（3）

【解析】

（1）连接OD，如图1，由圆周角定理可得∠AOD＝2∠AED＝90°，然后根据平行线的性质可得∠CDO＝∠AOD，再根据切线的判定方法即可证得结论；

（2）连接BE，如图2，由圆周角定理可得∠B＝∠ADE，然后在直角△ABE中利用∠ABE的正弦解答即可；

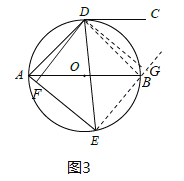
（3）如图3，作DG⊥直线EB于点G，连接DB，先证明ED平分∠AEB，再根据圆周角定理的推论和角平分线的性质得出：AD=BD，DF=DG，进一步即可根据HL证明Rt△ADF≌Rt△BDG，可得AF=BG，易证四边形DFEG是正方形，从而有EF=EG，然后根据线段间的和差关系即可推出结论．

（1）证明：连接OD，如图1，

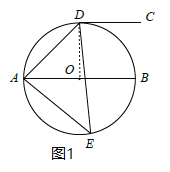
∵∠AED＝45°，

∴∠AOD＝2∠AED＝90°，

∵CD∥AB，

∴∠CDO＝∠AOD＝90°，即OD⊥CD，

∴直线CD与⊙O相切；

（2）解：连接BE，如图2，

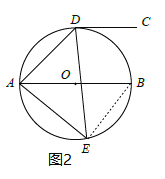
∵AB为⊙O的直径，∴∠AEB＝90°，

∵∠B＝∠ADE，∴sin∠ADE＝sinB，

∵sinB＝，⊙O的半径为，

∴，解得AE＝12；

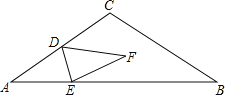
（3）如图3，作DG⊥直线EB于点G，连接DB，

∵∠AEB=90°，DF⊥AE，DG⊥EB，

∴四边形DFEG是矩形，

∵AB为⊙O的直径，∴∠AEB＝90°，

∵∠AED＝45°，∴∠BED＝45°，

∴∠AED＝∠BED，

∴，∴AD=BD，

∵DF⊥AE，DG⊥EB，∠AED＝∠BED，

∴DF=DG，

∴Rt△ADF≌Rt△BDG（HL），

∴AF=BG，

∵DF⊥AE，∠AED＝45°，

∴∠AED＝∠EDF＝45°，

∴DF=EF，

∴矩形DFEG是正方形，

∴EF=EG，

∴AE+BE=AF+EF+EG－BG=2EF=2DF．

故答案为：．