��Ŀ����
����Ŀ����ͼ��ֱ��y��x+c��x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��������y����x2+bx+c������A��C��
��1���������ߵĽ���ʽ��
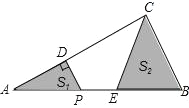
��2����֪��P���������ϵ�һ�����㣬���ҵ�P�ڵڶ������ڣ�������P��PE��x���ڵ�E�����߶�AC�ڵ�D��
����ͼ1����D��DF��y���ڵ�F������������M��N���㣨��Mλ�ڵ�N����ࣩ������EF�����߶�EF�ij������ʱ�����P��M��N�����ꣻ
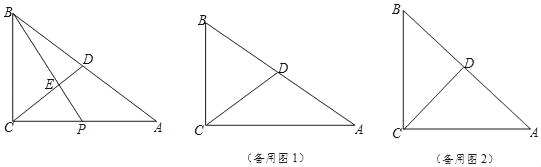
����ͼ2������CD������C��P��DΪ��������������ADE���ƣ����CPD�������

���𰸡���1��y����x2��3x+4����2������P����Ϊ����2��6������M��N������ֱ�Ϊ��![]() ��2������
��2������![]() ��2��������CPD�����Ϊ
��2��������CPD�����Ϊ![]() ��4��
��4��
��������
��1������A������ֱ����ֱ�ߺ������߱���ʽ��������⣻
��2�����ı���DEOFΪ���Σ��ʣ�EF��OD����OD��ֱ��ACʱ��OD��С����DΪAC���е㣬������Ϊ����2��2����������⣻
���֡�ADE�ס�CDP����ADE�ס�PCD�����������⼴�ɣ�
��1������A���������ֱ��y��x+c�ã�0����4+c��
��ã�c��4��
����A������������߱���ʽ�ã�0����16��4b+4��
��ã�b����3��
�������ߵı���ʽΪ��y����x2��3x+4��
�ʵ�A��C������ֱ�Ϊ����4��0������0��4����
��A��C���������һ�κ�������ʽy��kx+b�ã�
![]() �����
�����![]() ��
��
��ֱ��AC�ı���ʽΪ��y��x+4��
��2���١��ı���DEOFΪ���Σ��ʣ�EF��OD��
��OD��ֱ��ACʱ��OD��С����EF��С����
��OA��OC��
���DΪAC���е㣬������Ϊ����2��2����
�ʵ�P����Ϊ����2��6����
�ѵ�D�����������κ�������ʽ�ã���x2��3x+4��2��
��ã�x��![]() ��
��
�ʵ�M��N������ֱ�Ϊ��![]() ��2������
��2������![]() ��2����
��2����
�ڵ���ADE�ס�CDPʱ�����CPD��90����PC��PD��
��PC��x�ᣬ���P��������Ϊ4�����P����Ϊ����3��4����
��D��ֱ��AC��y��x+4�ϣ����D����Ϊ����3��1����
��PD��4��1��3��PC��
��S��CPD��![]() ��PCPD��
��PCPD��![]() ��
��
����ADE�ס�PDCʱ��
ͬ���ɵã�S��CPD��![]() ��PDCH��4��
��PDCH��4��
�ʣ���CPD�����Ϊ![]() ��4
��4

 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�