题目内容
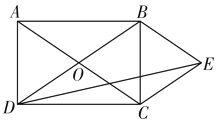
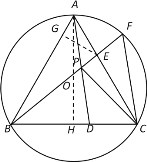
【题目】如图,已知⊙O是边长为6的等边△ABC的外接圆,点D,E分别是BC,AC上两点,且BD=CE,连接AD,BE相交于点P,延长线段BE交⊙O于点F,连接CF.


(1)求证:AD∥FC;
(2)连接PC,当△PEC为直角三角形时,求tan∠ACF的值.
【答案】(1)见解析;(2)当△PEC为直角三角形时,tan∠ACF=![]() 或
或![]()
【解析】
(1)先说明△ABD≌△BCE,然后再运用全等三角形的性质、圆周角的性质、角的和差以及平行线的判定定理解答即可;
(2)连接PC,分∠PCE=90°,∠CEP=90°和∠CPE=90°三种情况解答即可
解:(1)∵△ABC是等边三角形,

∴AB=BC=AC=2 , ∠ABC=∠ACB=∠BAC=60°,
∵BD=CE.
∴△ABD≌△BCE(SAS).
∴∠BAD=∠CBE.
∴∠BPD=∠BAD+∠ABP=∠CBE+∠ABP=60°
∵∠BAC=∠BFC=60°,
∴∠BPD=∠BFC.
∴AD∥FC.
(2) 当△PEC为直角三角形时,可分为三种情况:
∠PCE=90°或∠CEP=90°或∠CPE=90°.
①当∠PCE=90°时,
∵∠PCE<∠ACB=60°,
∴∠PCE=90°这种情况不存在.
②当∠CEP=90°时,
∵AB=BC=AC,
∴AE=EC,∠ABE=∠CBE=30°.
∴∠ACF=∠ABF=30°.
∴tan∠ACF=tan30°=![]() .
.
③当∠CPE=90°时,过点A作AH⊥BC于点H,
设AE=x,则CD=AE=x,CE=6-x.
∵AB=AC,AH⊥BC,
∴BH=CH=3,∠HAC=∠HAB=30°.
∴HD=3-x.
∵∠BFC=60°,∠CPE=90°,
∴∠PCF=∠HAC=30°.
∵AD∥FC,
∴∠FCA=∠DAC.
∴∠PCF-∠FCA=∠HAC-∠DAC.
∴∠HAD=∠PCE.
∵∠AHD=∠CPE=90°
∴△AHD∽△CPE.
∴![]() .
.

∴![]() ①.
①.
∵∠BPD=∠APE=∠ACB=60° ∠PAE=∠CAD
∴△PAE∽△CAD.
∴![]() .
.
∴![]() ②.
②.
观察①式和②式
可得:![]() .
.
∴![]() .
.
解得:x=2.
∴AE=2.
过点E作EG⊥AB于点G
∴在Rt△AEG中 ∠EAG=60°.
∴![]() .
.
![]() .
.
∴BG=AB-AG=5.
在Rt△BGE中,tan∠ABE=![]() .
.
∴tan∠ACF=tan∠ABE=![]() .
.
综上所述,当△PEC为直角三角形时,tan∠ACF=![]() 或
或![]() .
.