题目内容
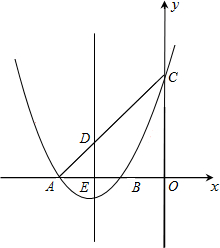
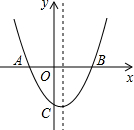
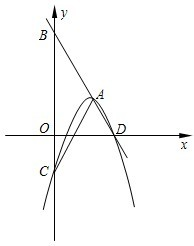
如图,半径为2的⊙C与x轴的正半轴交于点A,与y轴的正半轴交于点B,点C的坐标为(1,0).若抛物线y=-
x2+bx+c过A、B两点.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PBO=∠POB?若存在,求出点P的坐标;若不存在说明理由;
(3)若点M是抛物线(在第一象限内的部分)上一点,△MAB的面积为S,求S的最大(小)值.

| ||
| 3 |
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PBO=∠POB?若存在,求出点P的坐标;若不存在说明理由;
(3)若点M是抛物线(在第一象限内的部分)上一点,△MAB的面积为S,求S的最大(小)值.

(1)如答图1,连接CB.
∵BC=2,OC=1
∴OB=
=
∴B(0,
)
将A(3,0),B(0,
)代入二次函数的表达式
得
,解得
,
∴y=-
x2+
x+
.
(2)存在.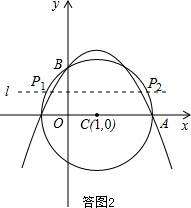
如答图2,作线段OB的垂直平分线l,与抛物线的交点即为点P1,P2.
∵B(0,
),O(0,0),
∴直线l的表达式为y=
.代入抛物线的表达式,
得-
x2+
x+
=
;
解得x1=1+
或x2=1-
,
∴P1(1-
,
)或P2(1+
,
).
(3)如答图3,作MH⊥x轴于点H.
设M(xm,ym),
则S△MAB=S梯形MBOH+S△MHA-S△OAB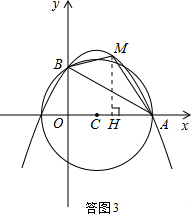
=
(MH+OB)•OH+
HA•MH-
OA•OB
=
(ym+
)xm+
(3-xm)ym-
×3×
=
xm+
ym-
∵ym=-
xm2+
xm+
,
∴S△MAB=
xm+
(-
xm2+
xm+
)-
=-
xm2+
xm
=-
(xm-
)2+
∴当xm=
时,S△MAB取得最大值,最大值为
.

∵BC=2,OC=1
∴OB=
| 4-1 |
| 3 |
∴B(0,
| 3 |
将A(3,0),B(0,
| 3 |
得
|
|
∴y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(2)存在.

如答图2,作线段OB的垂直平分线l,与抛物线的交点即为点P1,P2.
∵B(0,
| 3 |
∴直线l的表达式为y=
| ||
| 2 |
得-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| ||
| 2 |
解得x1=1+
| 1 |
| 2 |
| 10 |
| 1 |
| 2 |
| 10 |
∴P1(1-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(3)如答图3,作MH⊥x轴于点H.
设M(xm,ym),
则S△MAB=S梯形MBOH+S△MHA-S△OAB

=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
=
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∵ym=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
∴S△MAB=
| ||
| 2 |
| 3 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
=-
| ||
| 2 |
| 3 |
| 2 |
| 3 |
=-
| ||
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
| 3 |
∴当xm=
| 3 |
| 2 |
| 9 |
| 8 |
| 3 |


练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目