Question

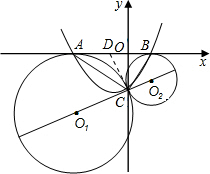
如图所示，⊙O₁和⊙O₂外切于点C，AB是⊙O₁和⊙O₂的外公切线，A、B为切点，且∠ACB=90°．以AB所在直线为轴，过点C且垂直于AB的直线为轴建立直角坐标系，已知AO=4，OB=1．
（1）分别求出A、B、C各点的坐标；
（2）求经过A、B、C三点的抛物线y=ax²+bx+c的解析式；
（3）如果⊙O₁的半径是5，问这条抛物线的顶点是否落在两圆连心线O₁O₂上？如果在，请证明；如果不在，请说明理由．

Answer 1

（1）∵AO=4，OB=1，
∴A、B两点的坐标分别为：（-4，0），（1，0），
∵∠ACB=90°，
设C点坐标为（0，y），则AB²=AC²+BC²，
即（|-4-1|）²=（-4）²+y²+1²+y²，
即25=17+2y²，解得y=2（舍去）或y=-2．
故C点坐标为（0，-2），

（2）设经过A、B、C三点的抛物线的函数解析式为y=ax²+bx+c，
则

16a-4b+c=0 a+b+c=0 c=-2

，
解得

a= 1 2 b= 3 2 c=-2

，
故所求二次函数的解析式为y=

1

2

x²+

3

2

x-2．

（3）过C作两圆的公切线CD交AB于D，则AD=BD=CD，由A（-4，0），B（1，0）可知D（-

3

2

，0），
设过CD两点的直线为y=kx+b，则

- 3 2 k+b=0 b=-2

，
解得

k=- 4 3 b=-2

，
故此一次函数的解析式为y=-

4

3

x-2，
∵过O₁，O₂的直线必过C点且与直线y=-

4

3

x-2垂直，
故过O₁，O₂的直线的解析式为y=

3

4

x-2．
由（2）中所求抛物线的解析式可知抛物线的顶点坐标为（-

3

2

，-

25

8

），
代入直线解析式得

3

4

×（-

3

2

）-2=-

25

8

，故这条抛物线的顶点落在两圆的连心O₁O₂上．