Question

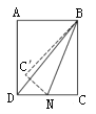
【题目】如图，在矩形ABCD中，AB=3，BC=4，点N为边DC上一动点（不与C、D重合），连接BN，作C关于直线BN的对称点C′连接B C′， C′N，当C′恰好在△ABD的边上时，CN的长为__________．

Answer 1

【答案】或

【解析】

分两种情况讨论：点C'在BD上或点C'在AD上，依据勾股定理以及折叠的性质，即可得到CN的长．

如图所示，当点C'在BD上时，

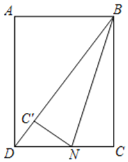
设CN=x，则C'N=x，DN=3-x，

由折叠可得，∠C=∠BC'N=90°，BC'=BC=4，

Rt△BCD中，BD= ，

∴C'D=5-4=1，

∴Rt△DC'N中，12+x2=（3-x）2，

解得x=；

如图所示，当点C'在AD上时，

设CN=x，则C'N=x，DN=3-x，

由折叠可得，BC'=BC=4，

Rt△ABC'中，AC'=，

∴C'D=，

∴Rt△DC'N中，()2+(3x)2＝x2，

解得x=；

综上所述，CN的长为或．

故答案为：或．