ƒøƒ⁄»ð
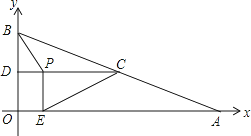
°æƒø°ø»ÁÕº£¨“ª¥Œ∫Ø ˝![]() µƒ∫Ø ˝ÕºœÒ”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„A°¢B£¨“‘œþ∂ŒABŒ™÷±Ω«±þ‘⁄µ⁄“ªœÛœÞƒ⁄◊˜Rt°˜ABC£¨«“ π°œABC£Ω30.
µƒ∫Ø ˝ÕºœÒ”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„A°¢B£¨“‘œþ∂ŒABŒ™÷±Ω«±þ‘⁄µ⁄“ªœÛœÞƒ⁄◊˜Rt°˜ABC£¨«“ π°œABC£Ω30.
£®1£©«Û°˜ABCµƒ√ʪ˝£ª
£®2£©»Áπ˚‘⁄µ⁄∂˛œÛœÞƒ⁄”–“ªµ„P£®m£¨![]() £©£¨ ‘”√∫¨mµƒ¥˙ ˝ Ω±Ì æÀƒ±þ–ŒAOPBµƒ√ʪ˝£¨≤¢«Ûµ±°˜APB”ΰ˜ABC√ʪ˝œýµ» ±mµƒ÷µ£ª
£©£¨ ‘”√∫¨mµƒ¥˙ ˝ Ω±Ì æÀƒ±þ–ŒAOPBµƒ√ʪ˝£¨≤¢«Ûµ±°˜APB”ΰ˜ABC√ʪ˝œýµ» ±mµƒ÷µ£ª
£®3£© «∑ҥʑ⁄ π°˜QAB «µ»—¸»˝Ω«–Œ≤¢«“‘⁄◊¯±Í÷·…œµƒµ„Q£ø»Ù¥Ê‘⁄£¨«Î–¥≥ˆQµƒÀ˘”–ø…ƒÐµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
°æ¥∞∏°ø£®1£©![]() £ª£®2£©SÀƒ±þ–ŒPOAB£Ω£≠
£ª£®2£©SÀƒ±þ–ŒPOAB£Ω£≠![]() m +
m + ![]() £ª
£ª![]() £ª£®3£©¥Ê‘⁄£¨£®3, 0£©£¨£®£≠1, 0£©£¨£®0£¨ £≠
£ª£®3£©¥Ê‘⁄£¨£®3, 0£©£¨£®£≠1, 0£©£¨£®0£¨ £≠![]() £©£¨£®0£¨
£©£¨£®0£¨![]() +2£©£¨£®0£¨
+2£©£¨£®0£¨![]() £≠2£©£¨£®0,£¨
£≠2£©£¨£®0,£¨![]() £©.
£©.
°æΩ‚Œˆ°ø
£®1£©œ»«Û≥ˆA°¢B¡Ωµ„µƒ◊¯±Í£¨‘Ÿ”…“ª∏ˆΩ«µ»”⁄30°„£¨«Û≥ˆACµƒ≥§£¨¥”∂¯º∆À„≥ˆ√ʪ˝£ª
£®2£©π˝P◊˜PD°Õx÷·£¨¥π◊„Œ™D£¨œ»«Û≥ˆÃð–ŒODPBµƒ√ʪ˝∫Õ°˜AOBµƒ√ʪ˝÷Æ∫Õ£¨‘Ÿºı»•°˜APDµƒ√ʪ˝£¨º¥ «°˜APBµƒ√ʪ˝£ª∏˘æð°˜APB”ΰ˜ABC√ʪ˝œýµ»£¨«Ûµ√mµƒ÷µ£ª
£®3£©ºŸ…˥ʑ⁄µ„Q£¨ π°˜QAB «µ»—¸»˝Ω«–Œ£¨«Û≥ˆQµ„µƒ◊¯±Íº¥ø…£Æ
£®1£©”…Ãıº˛÷™£∫![]()
°ý ‘⁄Rt°˜ABO÷–£¨![]()
‘⁄Rt°˜ABC÷–£¨°þ °œABC=30°„,
°ý![]()
°ý ![]()
£®2£©SÀƒ±þ–ŒPOAB£ΩS°˜OBP£´S°˜AOB
°þ ![]()
![]()
°ý SÀƒ±þ–ŒPOAB![]()
°þ ![]()
°ý S°˜APB£ΩSÀƒ±þ–ŒPOAB£≠S°˜AOP![]()
µ±S°˜APB£Ω![]() ±
± ![]()
°ý ![]()
(3)°þ![]()
°ýµ±AQ=AB ±,µ„![]()
µ±AB=BQ ±,µ„![]()
µ±AQ=BQ ±,µ„![]()
◊€…œø…µ√£∫![]()