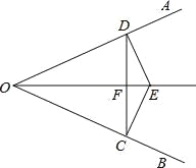
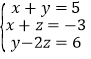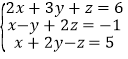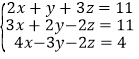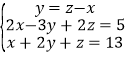题目内容
【题目】探索三角形的内角与外角平分线(三角形的外角是三角形的一边与另一边的延长线所组成的角):
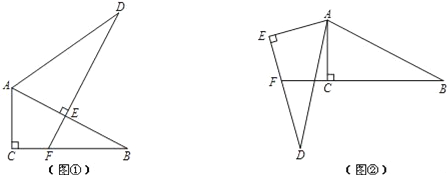
(1)如图①,在△ABC中,BO平分∠ABC,CO平分∠ACB,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(2)如图②,BO平分∠ABC,CO平分∠ACE,若∠A=50°,则∠BOC=________;此时∠A与∠BOC有怎样的关系?试说明理由.
(3)如图③,△ABC的外角∠CBE,∠BCF的平分线BO,CO相交于点O,若∠A=50°,则∠BOC=______;此时∠A与∠BOC有怎样的关系?(不需说明理由)
【答案】(1)115°,∠BOC=90°+![]() ∠A,.理由见解析;(2)25°,∠BOC=
∠A,.理由见解析;(2)25°,∠BOC=![]() ∠A,理由见解析;(3)65°,∠BOC=90°-
∠A,理由见解析;(3)65°,∠BOC=90°-![]() ∠A.
∠A.
【解析】
(1)根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB,则2∠BOC=360°-2∠OBC-2∠OCB,再根据角平分线的定义得∠ABC=2∠OBC,∠ACB=2∠OCB,则2∠BOC=360°-∠ABC-∠ACB,易得∠BOC=90°+![]() ∠A.
∠A.
(2)根据角平分线的定义得∠ACE=2∠OCE,∠ABC=2∠OBC,由三角形外角的性质有∠OCE=∠BOC+∠OBC,∠ACE=∠ABC+∠A,则2∠BOC+2∠OBC=∠ABC+∠A,即可得到∠BOC=![]() ∠A;
∠A;
(3)根据三角形内角和定理和外角性质可得到∠BOC=90°-![]() ∠A.
∠A.
(1)115° ∠BOC=90°+![]() ∠A.理由如下:
∠A.理由如下:
∵∠BOC=180°-∠OBC-∠OCB,
∴2∠BOC=360°-2∠OBC-2∠OCB.
而BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴2∠BOC=360°-(∠ABC+∠ACB).
∵∠ABC+∠ACB=180°-∠A,
∴2∠BOC=180°+∠A,
∴∠BOC=90°+![]() ∠A.
∠A.
(2)25° ∠BOC=![]() ∠A.理由如下:
∠A.理由如下:
∵CO平分∠ACE,
∴∠ACE=2∠OCE.
∵∠OCE=∠OBC+∠BOC,
∠ACE=∠ABC+∠A,
∴∠ABC+∠A=2∠OBC+2∠BOC.
∵BO平分∠ABC,∴∠ABC=2∠OBC,
∴2∠OBC+∠A=2∠OBC+2∠BOC,
∴∠A=2∠BOC,即∠BOC=![]() ∠A.
∠A.
(3)65° ∠BOC=90°-![]() ∠A.
∠A.