题目内容
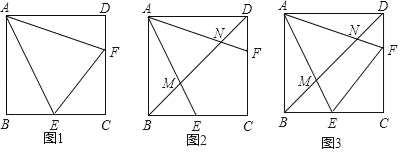
【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.
【答案】(1)证明见解析;(2)①5;②证明见解析.
【解析】
(1)延长CB到G,使GB=DF,连接AG,求证△ABG≌△ADF,得∠3=∠2,AG=AF,进而求证△AGE≌△AFE,可得GB+BE=EF,所以DF+BE=EF.
(2)①如图2,把△ABM绕点A逆时针旋转90°得到△ADM′,连接NM′.就可以得出△ABM≌△ADM′,就有∠BAM=∠DAM′,就可以得出△AMN≌△AM′N就可以得出MN=M′N,由勾股定理就可以得出结论MN2=DN2+BM2;
②设正方形ABCD的边长为a,求出MN,EC即可判断;
(1)证明:证明:延长CB到G,使GB=DF,连接AG(如图1),
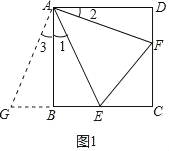
∵AB=AD,∠ABG=∠D=90°,GB=DF,
∴△ABG≌△ADF(SAS),
∴∠3=∠2,AG=AF,
∵∠BAD=90°,∠EAF=45°,
∴∠1+∠2=45°,
∴∠GAE=∠1+∠3=45°=∠EAF,
∵AE=AE,∠GAE=∠EAF,AG=AF,
∴△AGE≌△AFE(SAS),
∴GB+BE=EF,
∴DF+BE=EF;
(2)①解:如图2,在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠ABM=∠ADN=45°.
把△ABM绕点A逆时针旋转90°得到△ADM'.连结NM'.
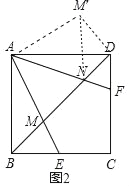
∴△ABM≌△ADM′(旋转不变性),
∴DM'=BM,AM'=AM,∠ADM'=∠ABM=45°,∠DAM'=∠BAM.
∴∠ADB+∠ADM′=45°+45°=90°,
即∠NDM′=90°.
∵∠EAF=45°,
∴∠BAM+∠DAN=45°,
∴∠DAM′+∠DAF=45°,
即∠M′AN=45°,
∴∠M'AN=∠MAN.
在△AMN和△AM′N中
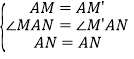 ,
,
∴△AMN≌△AM′N(SAS),
∴M'N=MN.
∵∠NDM′=90°,
∴M'N2=DN2+DM'2,
∴MN2=DN2+BM2;
设MN=x,则DN=12﹣3﹣x=9﹣x,
∴x2=33+(9﹣x)2,
∴x=5,
∴NM=5;
②证明:如图3中,设正方形ABCD的边长为a.
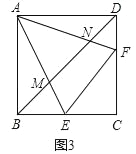
∵EF∥BD,
∴∠CEF=∠CBD=45°,∠CFE=∠CDB=45°,
∴∠CEF=∠CFE=45°,
∴CE=CF,
∴BE=DF,
∵AB=AD,∠ABE=∠ADF,BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,
∵∠EAF=45°,
∴∠BAE=∠DAF=22.5°,
∴∠AEB=∠BME=67.5°,
∴BM=BE,同理可证:DN=DF,
∴BM=DN=BE=DF,设BM=x,则MN=![]() x,
x,
∴2x+![]() x=
x=![]() a,
a,
∴x=(![]() ﹣1)a,
﹣1)a,
∴MN=(2﹣![]() )a,EC=BC﹣BE=(2﹣
)a,EC=BC﹣BE=(2﹣![]() )a,
)a,
∴MN=EC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某种蔬菜的价格随季节变化如下表,根据表中信息,下列结论错误的是( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
价格 | 5.00 | 5.50 | 5.00 | 4.80 | 2.00 | 1.50 | 1.00 | 0.90 | 1.50 | 3.00 | 2.50 | 3.50 |
A. ![]() 是自变量,
是自变量,![]() 是因变量
是因变量
B. 2月份这种蔬菜价格最高,为5.50元/千克
C. 2-8月份这种蔬菜价格一直在下降
D. 8-12月份这种蔬菜价格一直在上升