题目内容
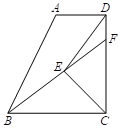
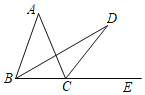
【题目】如图,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,∠D=15°,则∠A=__.
【答案】30°
【解析】
先根据角平分线的定义得到∠ABD=∠CBD,∠ACD=∠ECD,再根据三角形外角性质得∠ACE=∠A+∠ABC,代入得:∠A=2(∠ECD﹣∠CBD),可得结论.
∵∠ABC的平分线与∠ACE的平分线交于点D,
∴∠ABD=∠CBD,∠ACD=∠ECD,
∵∠ACE=∠A+∠ABC,
即∠ACD+∠ECD=∠ABC+∠CBD+∠A,
∴2∠ECD=2∠CBD+∠A,
∴∠A=2(∠ECD﹣∠CBD)
∵∠ECD=∠CBD+∠D,∠D=15°
∴∠D=∠ECD﹣∠CBD=15°
∴∠A=2×15°=30°.
故答案为:30°.

练习册系列答案
相关题目