题目内容
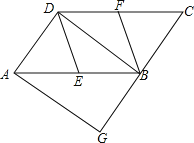
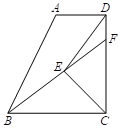
【题目】如图,在四边形ABCD中,∠ADC=∠BCD=90°,BC=CD=2AD,E为∠BCD平分线上的点,连接BE、DE, 延长BE交CD于点F.
⑴ 求证:△BCE≌△DCE;
⑵ 若DE∥AB,求证:FD=FC.
【答案】证明见解析
【解析】(1)由角平分线的性质可得∠BCE=∠DCE,再由BC=CD,CE=CE ,可得出结果;(2) 延长DE交BC于G,由AD∥BC, DE∥AB推出四边形ABGD是平行四边形,再利用ASA证明△DFE≌△BGE,从而得证.
⑴ ∵CE平分∠BCD,
∴∠BCE=∠DCE
又BC=CD,CE=CE,
∴△BCE≌△DCE
⑵ 延长DE交BC于G
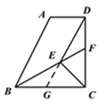
∵AD∥BC, DE∥AB,
∴四边形ABGD是平行四边形,
∴BG=AD=![]()
可证得△DFE≌△BGE
∴FD=BG=![]() ∴FD=FC.
∴FD=FC.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目