题目内容
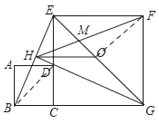
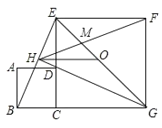
【题目】如图，正方形ABCD的边CD在正方形ECGF的边CE上，O是EG的中点，∠EGC的平分线GH过点D，交BE于点H，连接OH，FH，EG与FH交于点M，对于下面四个结论：①GH⊥BE；②BG＝EG；③△MFG为等腰三角形；④DE：AB＝1＋
:1，其中正确结论的序号为_________．
【答案】①②③
【解析】
证明△BCE≌△DCG，即可证得∠BEC＝∠DGC，然后根据三角形的内角和定理证得∠EHG＝90°，则HG⊥BE，然后证明△BGH≌△EGH，可得BG＝EG，H是BE的中点，则OH是△BGE的中位线，根据三角形的中位线定理即可得到HO＝
BG，HO∥BG，以及∠MOH＝∠EGC＝45°，再根据等腰直角三角形的性质，得出OF＝EG，∠OFG＝45°，以及OH＝OF，根据∠MHO＋∠HOM＝∠OFH＋∠OFG，即可得出∠FMG＝∠MFG，最后根据等腰直角三角形的边角关系，得出DB：AB＝
：1，即可得到DE：AB＝：1．
∵正方形ABCD的边CD在正方形ECGF的边CE上，
∴∠BCE＝∠DCG＝90°，BC＝DC，EC＝GC，
∴△BCE≌△DCG（SAS），
∴∠CGD＝∠CEB，
又∵∠CDG＝∠HDE，
∴∠EHD＝∠GCD＝90°，
∴GH⊥BE，故①正确；
∵∠EGC的平分线GH过点D，
∴∠BGH＝∠EGH，
∵GH⊥BE，
∴∠BHG＝∠EHG＝90°，
∵GH=GH，
∴△BGH≌△EGH（ASA），
∴BG＝EG，故②正确；
∵BG＝EG，GH⊥BE，
∴H为BE的中点，
又∵O是EG的中点，
∴HO是△BEG的中位线，
∴HO＝BG，HO∥BG，
∴∠MOH＝∠EGC＝45°，
如图，连接FO，
∵O是EG的中点，
∴等腰Rt△EFG中，OF＝EG，∠OFG＝45°，
∴OH＝OF，
∴∠OHF＝∠OFH，
∴∠MHO＋∠HOM＝∠OFH＋∠OFG，即∠FMG＝∠MFG，
∴FG＝MG，即△MFG是等腰三角形，故③正确；
如图，连接BD，
∵HG垂直平分BE，
∴DE＝DB，
∵Rt△ABD中，DB：AB＝：1，
∴DE：AB＝：1，故④错误；
故答案为：①②③
