题目内容
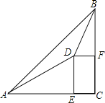
【题目】如图，在小山的东侧A庄，有一热气球，由于受西风的影响，以每分钟35 m的速度沿着与水平方向成75°角的方向飞行，40 min时到达C处，此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上，同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°，求A庄与B庄的距离及山高(结果保留根号)．
【答案】A庄与B庄的距离是1 400
m，山高是700(
－)m.
【解析】
此题要先作AD⊥BC于D，PE⊥AB于E，则先求得AC的长，再求得AD的长、AB的长，然后在△PBA中，利用∠B和∠PAB的值求得PE的长．
解：过点A作AD⊥BC，垂足为D.
在Rt△ADC中，∠ACD＝75°－30°＝45°，AC＝35×40＝1 400(m)．
∴AD＝AC·sin 45°＝1 400×
＝700 (m)．
在Rt△ABD中，∠B＝30°，
∴AB＝2AD＝1 400m.
又过点P作PE⊥AB，垂足为E，
则AE＝PE，BE＝
＝
PE.
∴(＋1)PE＝1 400.
解得PE＝700(－)m.
答：A庄与B庄的距离是1 400 m，山高是700(－)m.
练习册系列答案
相关题目
