Question

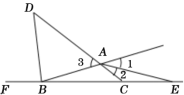
【题目】抛物线y1=ax2+c与x轴交于A、B两点，与y轴交于点C，点P在抛物线上，过P（1，﹣3），B（4，0）两点作直线y2=kx+b．

（1）求a、c的值；

（2）根据图象直接写出y1＞y2时，x的取值范围；

（3）在抛物线上是否存在点M，使得S△ABP=5S△ABM，若存在，求出点M的坐标，若不存在，请说明理由．

Answer 1

【答案】（1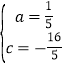）；（2）x＞4或x＜1；（3）M点的坐标是（，）（﹣，）（，﹣）（﹣，﹣）．

【解析】

由B、P两点的坐标，利用待定系数法可求得a、c；以P、B的横坐标为分界点，直接写出y1＞y2时x的取值范围；假定M点的纵坐标为e,根据S△ABP=5S△ABM，可求出M的坐标.

（1）将P（1，﹣3）、B（4，0）代入y=ax2+c得：，

解得：；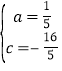

（2）由图象得x＞4或x＜1；

（3）在抛物线上存在点M，使得S△ABP=5S△ABM，

理由是：抛物线的解析式是y=x2﹣，

设M点的纵坐标为e，

∵P（1，﹣3），

∴由S△ABP=5S△ABM得：×AB×|﹣3|=5××AB×|e|，

解得；|e|=，

当e=时， x2﹣=，

解得：x=±，

当e=﹣时， x2﹣=﹣，

解得：x=±，

即M点的坐标是（，）（﹣，）（，﹣）（﹣，﹣）．