题目内容
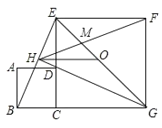
【题目】如图1,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.

(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论,_____________.
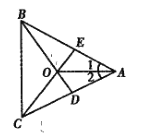
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度![]() ,得到如图2的情形,BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,证明你的判断.
,得到如图2的情形,BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,证明你的判断.
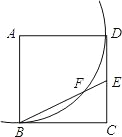
(3)将图1中的正方形CDEF,绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,得到如图3的情形,点
,得到如图3的情形,点![]() 恰好落在斜边
恰好落在斜边![]() 上,若
上,若![]() ,求正方形CDEF的边长.
,求正方形CDEF的边长.
【答案】(1)BF=AD,BF⊥AD;(2)结论仍然成立.理由见解析(3)2![]() .
.
【解析】
(1)根据等腰直角三角形的性质得CA=CB,再根据正方形的性质得CF=CD,∠ACD=90°,根据旋转的定义得到把△CBF绕点C顺时针旋转90°可得到△CAD,然后根据旋转的性质得BF=AD,BF⊥AD.
(2)由(1)得CB=CA,CF=CD,∠BCA=∠FCD=90°,易得∠BCF=∠ACD,所以把△CBF绕点C顺时针旋转90°可得到△CAD,根据旋转的性质得BF=AD,BF⊥AD;
(3)如图4,作EH⊥AC于H,连结CE,由于将图1中的正方形CDEF,绕着点C按逆时针方向旋转105°,根据旋转的性质得∠ACD=105°90°=15°;再根据正方形的性质得∠ECD=45°,则∠ACE=60°,而△ABC为等腰直角三角形,则∠A=45°;在Rt△CEH中,设CH=x,根据含30度的直角三角形三边的关系得CE=2x,EH=![]() x,在Rt△AEH中,根据等腰直角三角形的性质得AH=EH=
x,在Rt△AEH中,根据等腰直角三角形的性质得AH=EH=![]() x,则AH+CH=
x,则AH+CH=![]() x+x,所以
x+x,所以![]() x+x=2
x+x=2![]() +2,解得x=2,则CE=2x=4,然后根据等腰直角三角形的性质计算出CD=
+2,解得x=2,则CE=2x=4,然后根据等腰直角三角形的性质计算出CD=![]() CE=2
CE=2![]() .
.
(1)∵△ABC为等腰直角三角形,∠ACB=90°,
∴CA=CB,
∵四边形CDEF为正方形,
∴CF=CD,∠ACD=90°,
∴把△CBF绕点C顺时针旋转90°可得到△CAD,
∴BF=AD,BF⊥AD.
故答案为BF=AD,BF⊥AD;
(2)(1)中得到的结论仍然成立.理由如下:
由(1)得CB=CA,CF=CD,∠BCA=∠FCD=90°,
∴∠BCA+∠ACF=∠ACF+∠FCD,即∠BCF=∠ACD,
∴把△CBF绕点C顺时针旋转90°可得到△CAD,
∴BF=AD,BF⊥AD;
(3)如图4,作EH⊥AC于H,连结CE,
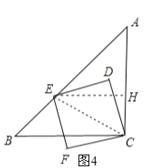
∵将图1中的正方形CDEF,绕着点C按逆时针方向旋转105°,
∴∠ACD=105°90°=15°,
∵四边形CDEF为正方形,
∴∠ECD=45°,
∴∠ACE=45°+15°=60°,
∴∠A=45°,
在Rt△CEH中,设CH=x,则CE=2x,
∴EH=![]() =
=![]() x,
x,
在Rt△AEH中,AH=EH=![]() x,
x,
∴AH+CH=![]() x+x,
x+x,
而AC=2![]() +2,
+2,
∴![]() x+x=2
x+x=2![]() +2,解得x=2,
+2,解得x=2,
∴CE=2x=4,
∵△CED为等腰直角三角形,
∴CD=![]() CE=2
CE=2![]() ,
,
即正方形CDEF的边长为2![]() .
.