ЬтФПФкШн
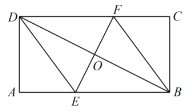
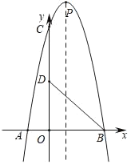
ЁОЬтФПЁПвбжЊЃЌШчЭМХзЮяЯпyЃНax2+3ax+cЃЈaЃО0ЃЉгыyжсНЛгкЕуCЃЌгыxжсНЛгкAЃЌBСНЕуЃЌЕуAдкЕуBзѓВрЃЎЕуBЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЎOCЃН3OBЃЎ
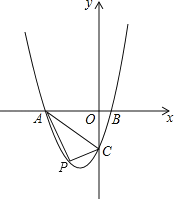
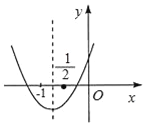
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPЪЧЯпЖЮACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЌЧѓШ§НЧаЮPACУцЛ§ЕФзюДѓжЕЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЁїPACЕФУцЛ§ЮЊSЃЌЦфжаSЮЊећЪ§ЕФЕуPзїЁАКУЕуЁБЃЌдђДцдкЖрИіЁАКУЕуЁБЃЌдђЫљгаЁАКУЕуЁБЕФИіЪ§ЮЊЁЁ ЁЁ
ЃЈ4ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌвдPAЮЊБпЯђжБЯпACгвЩЯВрзїе§ЗНаЮAPHGЃЌЫцзХЕуPЕФдЫЖЏЃЌе§ЗНаЮЕФДѓаЁЁЂЮЛжУвВЫцжЎИФБфЃЌЕБЖЅЕуHЛђGЧЁКУТфдкyжсЩЯЪБЃЌжБНгаДГіЖдгІЕФЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФБэДяЪНЮЊЃКyЃН![]() x2+
x2+![]() xЉ6ЃЛ
xЉ6ЃЛ
ЃЈ2ЃЉЕБxЃНЉ![]() ЪБЃЌSЕФзюДѓжЕЮЊЃК
ЪБЃЌSЕФзюДѓжЕЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ4ЃЛ
ЃЈ4ЃЉЕуPЕФзјБъЮЊЃКЃЈ![]() ЃЌЉ5ЃЉЛђЃЈ
ЃЌЉ5ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШШЗЖЈЕуCЕФзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтЃЛ
ЃЈ2ЃЉЯШЧѓГіжБЯпACЕФНтЮіЪНЃЌдйЙ§ЕуPзїyжсЕФЦНааЯпНЛACгкЕуHЃЌЩшЕуPЕФКсзјБъЮЊxЃЌгЩгкЁїPACУцЛ§SЃН![]() PHЁСOAЃЌЧвOAвзЧѓЃЌжЛашгУКЌxЕФДњЪ§ЪНБэЪОГіPHЕФГЄМДПЩРћгУЖўДЮКЏЪ§ЕФаджЪЧѓГіНсЙћЃЛ
PHЁСOAЃЌЧвOAвзЧѓЃЌжЛашгУКЌxЕФДњЪ§ЪНБэЪОГіPHЕФГЄМДПЩРћгУЖўДЮКЏЪ§ЕФаджЪЧѓГіНсЙћЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЬтЕФЙиЯЕЪНВЂНсКЯxЕФЗЖЮЇж№вЛбщжЄSЪЧЗёЮЊећЪ§МДЕУД№АИЃЛ
ЃЈ4ЃЉЗжЕуGдкyжсЩЯКЭЕуHдкyжсЩЯСНжжЧщПіЃЌРћгУе§ЗНаЮЕФаджЪЙЙдьШЋЕШШ§НЧаЮЗжБ№ЧѓНтМДПЩ.
НтЃКЃЈ1ЃЉOCЃН3OBЃН6ЃЌЙЪЕуBЁЂCЕФзјБъЗжБ№ЮЊЃКЃЈ2ЃЌ0ЃЉЁЂЃЈ0ЃЌЉ6ЃЉЃЌдђХзЮяЯпЮЊyЃНax2+3axЉ6ЃЌ
НЋЕуBЕФзјБъДњШыЩЯЪНЕУЃК0ЃН4a+6aЉ6ЃЌНтЕУЃКaЃН![]() ЃЌ
ЃЌ
ЙЪХзЮяЯпЕФБэДяЪНЮЊЃКyЃН![]() x2+
x2+![]() xЉ6ЃЛ
xЉ6ЃЛ
ЃЈ2ЃЉyЃН![]() x2+
x2+![]() xЉ6ЃЌСюyЃН0ЃЌдђxЃНЉ5Лђ2ЃЌЙЪЕуAЃЈЉ5ЃЌ0ЃЉЃЌ
xЉ6ЃЌСюyЃН0ЃЌдђxЃНЉ5Лђ2ЃЌЙЪЕуAЃЈЉ5ЃЌ0ЃЉЃЌ
НЋЕуAЁЂCЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНЃКyЃНkx+bВЂНтЕУЃКжБЯпACЕФНтЮіЪНЮЊЃКyЃНЉ![]() xЉ6ЃЌ
xЉ6ЃЌ
Й§ЕуPзїyжсЕФЦНааЯпНЛACгкЕуHЃЌ

ЩшЕуPЃЈxЃЌ![]() x2+
x2+![]() xЉ6ЃЉЃЌЕуHЃЈxЃЌЉ
xЉ6ЃЉЃЌЕуHЃЈxЃЌЉ![]() xЉ6ЃЉЃЌ
xЉ6ЃЉЃЌ
ЁїPACУцЛ§SЃН![]() PHЁСOAЃН
PHЁСOAЃН![]() ЃНЉ
ЃНЉ![]() x2Љ
x2Љ![]() x
x![]() ЃЌ
ЃЌ
ЁпЉ![]() <0ЃЌЙЪSгазюДѓжЕЃЌ ЕБxЃНЉ
<0ЃЌЙЪSгазюДѓжЕЃЌ ЕБxЃНЉ![]() ЪБЃЌSЕФзюДѓжЕЮЊЃК
ЪБЃЌSЕФзюДѓжЕЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁїPACУцЛ§SЃНЉ![]() x2Љ
x2Љ![]() xЃЌвђЮЊЕуPЪЧЯпЖЮACЯТЗНХзЮяЯпЩЯЕФЕуЃЌЫљвдЃ5<x<0ЃЌ
xЃЌвђЮЊЕуPЪЧЯпЖЮACЯТЗНХзЮяЯпЩЯЕФЕуЃЌЫљвдЃ5<x<0ЃЌ
ЕБxЃНЉ4ЪБЃЌSЃН6ЃЛЕБxЃНЉ3ЪБЃЌsЃН9ЃЛЕБxЃНЉ2ЪБЃЌS=9ЃЛЕБxЃНЉ1ЪБЃЌsЃН6ЃЛ
ЫљвдЁАКУЕуЁБЕФИіЪ§ЮЊ4ЃЌ
ЙЪД№АИЮЊ4ЃЛ
ЃЈ4ЃЉШчЭМ2зѓВрЭМЃЌ
ЂйЕБЕуGдкyжсЩЯЪБЃЌзїPRЁЭxжсгкЕуRЃЌ
ЁпЁЯGAO+ЁЯPAOЃН90ЁуЃЌЁЯPAO+ЁЯAPRЃН90ЁуЃЌ
ЁрЁЯAPRЃНЁЯGAOЃЌ
ЁпЁЯAOGЃНЁЯPRAЃН90ЁуЃЌAPЃНAGЃЌ
ЁрЁїAOGЁеЁїPRAЃЈAASЃЉЃЌ
ЁрOAЃНPRЃН5ЃЌ
ЙЪЕуPЕФзнзјБъЮЊЃКЉ5ЃЌ
дђyЃН![]() x2+
x2+![]() xЉ6ЃНЉ5ЃЌНтЕУЃКxЃН
xЉ6ЃНЉ5ЃЌНтЕУЃКxЃН![]() ЃЈВЛКЯЬтвтЕФжЕвбЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЕФжЕвбЩсШЅЃЉЃЌ
ЙЪЕуPЃЈ![]() ЃЌЉ5ЃЉЃЛ
ЃЌЉ5ЃЉЃЛ

ЂкЕБЕуHдкyжсЩЯЪБЃЌЭМ2гвВрЭМЃЌЭЌРэПЩЕУЃКЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЃЌЕуPЕФзјБъЮЊЃКЃЈ![]() ЃЌЉ5ЃЉЛђЃЈ
ЃЌЉ5ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ

 ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИ
ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИЁОЬтФПЁПФГЩЬЕъЗжСНДЮЙКНј![]() ЁЂ
ЁЂ![]() СНжжЩЬЦЗНјааЯњЪлЃЌСНДЮЙКНјЭЌвЛжжЩЬЦЗЕФНјМлЯрЭЌЃЌОпЬхЧщПіШчЯТБэЫљЪОЃК
СНжжЩЬЦЗНјааЯњЪлЃЌСНДЮЙКНјЭЌвЛжжЩЬЦЗЕФНјМлЯрЭЌЃЌОпЬхЧщПіШчЯТБэЫљЪОЃК
ЙКНјЪ§СПЃЈМўЃЉ | ЙКНјЫљашЗбгУ ЃЈдЊЃЉ | ||
A | B | ||
ЕквЛДЮ | 20 | 50 | 4100 |
ЕкЖўДЮ | 30 | 40 | 3700 |
ЃЈ1ЃЉЧѓ![]() ЁЂ
ЁЂ![]() СНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧЖрЩйдЊЃП
СНжжЩЬЦЗУПМўЕФНјМлЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЩЬГЁОіЖЈ![]() ЩЬЦЗвдУПМў50дЊГіЪлЃЌ
ЩЬЦЗвдУПМў50дЊГіЪлЃЌ![]() ЩЬЦЗвдУПМў
ЩЬЦЗвдУПМў![]() дЊГіЪлЃЎЮЊТњзуЪаГЁашЧѓЃЌашЙКНј
дЊГіЪлЃЎЮЊТњзуЪаГЁашЧѓЃЌашЙКНј![]() ЁЂ
ЁЂ![]() СНжжЩЬЦЗЙВ
СНжжЩЬЦЗЙВ![]() МўЃЌЧв
МўЃЌЧв![]() ЩЬЦЗЕФЪ§СПВЛЩйгк
ЩЬЦЗЕФЪ§СПВЛЩйгк![]() ЩЬЦЗЪ§СПЕФ
ЩЬЦЗЪ§СПЕФ![]() БЖЃЌЧыФуЧѓГіЛёРћзюДѓЕФНјЛѕЗНАИЃЌВЂШЗЖЈзюДѓРћШѓЃЎ
БЖЃЌЧыФуЧѓГіЛёРћзюДѓЕФНјЛѕЗНАИЃЌВЂШЗЖЈзюДѓРћШѓЃЎ