题目内容
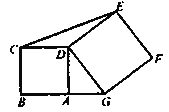
【题目】如图,A在线段BG上,ABCD和DEFG都是正方形,面积分别为7和11,则△CDE的面积等于 .
【答案】![]()
【解析】
过E点和G点分别作△CDE和△DGF的高CP和GH,证明△DCP与△DGH全等,得出CP=DH,再根据勾股定理求出DH=AG,通过求三角形的面积可得到答案.
过E点和G点分别作△CDE和△DGF的高CP和GH,
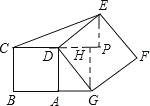
∵DGFC是正方形,
∴DG=DE,∠EDG=90°,
∵∠EDP+∠HDG=90°
∵∠EDP+∠DEP=90°,
∴∠HDG=∠DEP,
在△EDP与△DGH中,
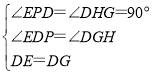
∴△EDP≌△DGH(AAS),
∴DH=PE,
∵∠DAG=∠DHG=90°,∠ADH=∠AGH=90°
∴四边形ADHG是矩形,
∴AG=DH,
∵正方形ABCD和正方形DEFG的面积分别为7和11,
∴CD=AD=![]() ,DG=
,DG=![]() ,
,
在Rt△ADG中,
AG=![]() ,
,
∴PE=2,
∴△CDE的面积=![]() CDPE=
CDPE=![]() ×
×![]() ×2=
×2=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目