Question

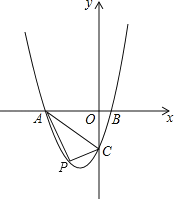
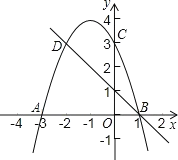
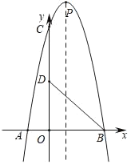
【题目】如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+8与x轴相交于点A（﹣2，0）和点B（4，0），与y轴相交于点C，顶点为点P．点D（0，4）在OC上，联结BC、BD．

（1）求抛物线的表达式并直接写出点P的坐标；

（2）点E为第一象限内抛物线上一点，如果△COE与△BCD的面积相等，求点E的坐标；

（3）点Q在抛物线对称轴上，如果△BCD∽△CPQ，求点Q的坐标．

Answer 1

【答案】（1）点P的坐标为（1，9）；（2）点E的坐标为（2，8）；（3）点Q的坐标为（1，11）或（1，10）．

【解析】

（1）通过待定系数法代入A、B坐标即可求得解析式；

（2）根据解析式可求得点C坐标（0，8），根据点E为第一象限内抛物线上一点设点E（（x，﹣x2+2x+8）再根据S△COE＝S△BCD，可求得E点坐标.

（3）根据点B、D的坐标可得到∠BDC＝135°，要满足△BCD∽△CPQ，∠CPQ=135°或者∠PCQ=135°，通过点C、P的坐标可得，∠PCM＝45°，所以∠MCQ=90°，Q在对称轴上，此情况不成立，所以要满足△BCD∽△CPQ，仅∠CPQ=135°，即Q在P点上方，可分两类讨论，或代值即可求出Q点坐标.

（1）将点A（﹣2，0），B（4，0）代入y＝ax2+bx+8，得：

解得：，

∴抛物线的表达式为y＝﹣x2+2x+8．

∵y＝﹣x2+2x+8＝﹣（x﹣1）2+9，

∴点P的坐标为（1，9）．

（2）当x＝0时，y＝﹣x2+2x+8＝8，

∴点C的坐标为（0，8）．

设点E的坐标为（x，﹣x2+2x+8）（0＜x＜4），

∵S△COE＝S△BCD，

∴×8x＝×4×4，

解得：x＝2，

∴点E的坐标为（2，8）．

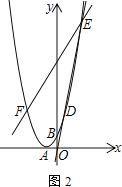
（3）过点C作CM∥x轴，交抛物线对称轴于点M，如图所示．

∵点B（4，0），点D（0，4），

∴OB＝OD＝4，

∴∠ODB＝45°，BD＝4，

∴∠BDC＝135°．

∵点C（0，8），点P（1，9），

∴点M的坐标为（1，8），

∴CM＝PM＝1，

∴∠CPM＝45°，CP＝，

∴点Q在抛物线对称轴上且在点P的上方，

∴∠CPQ＝∠CDB＝135°．

∵△BCD∽△CPQ，

∴或．

①当时，，

解得：PQ＝2，

∴点Q的坐标为（1，11）；

②当时，，

解得：PQ＝1，

∴点Q的坐标为（1，10）．

综上所述，点Q的坐标为（1，11）或（1，10）．