题目内容
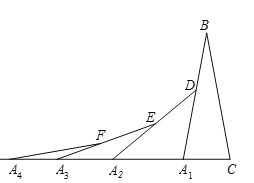
【题目】如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,按此做法继续下去,第2019个等腰三角形的底角度数是______________.
【答案】![]()
【解析】
根据等腰三角形的性质求出∠BA1C的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律即可得出第2019个三角形中以A2019为顶点的内角度数.
解:∵在△CBA1中,∠B=20°,A1B=CB,
∴∠BA1C=![]() =80°,
=80°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=![]() ∠BA1C=
∠BA1C=![]() ×80°;
×80°;
同理可得∠EA3A2=(![]() )2×80°,∠FA4A3=(
)2×80°,∠FA4A3=(![]() )3×80°,
)3×80°,
∴第n个三角形中以An为顶点的底角度数是(![]() ) n-1×80°.
) n-1×80°.
∴第2017个三角形中以A2019为顶点的底角度数是(![]() )2018×80°,
)2018×80°,
故答案为:(![]() ) 2018×80°.
) 2018×80°.

 名校课堂系列答案
名校课堂系列答案【题目】某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90天的销售单价p(元/kg)与时间t(天)之间的相关信息如图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如表,设第t天销售利润为w(元)
时间t(天) | 10 | 30 |
每天的销售量 y(kg) | 180 | 140 |
(1)分别求出售单价p(元/kg)、销售量y(kg)与时间t(天)之间的函数关系式;
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;

【题目】行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得数据如下表:
刹车时车速/km·h-1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
刹车距离/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象.估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5 m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?



