题目内容
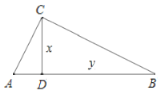
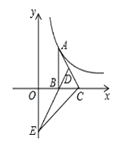
【题目】如图，已知点A在反比例函数
的图象上，作
，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，若
的面积为6，则k=___．
【答案】12
【解析】
先根据题意证明△BOE∽△CBA，根据相似比及面积公式得出BO×AB的值即为|k|的值，再由函数所在的象限确定k的值．
∵BD为Rt△ABC的斜边AC上的中线，
∴BD=DC，∠DBC=∠ACB，
又∠DBC=∠EBO，
∴∠EBO=∠ACB，
又∠BOE=∠CBA=90°，
∴△BOE∽△CBA，
∴
，即BC×OE=BO×AB．
又∵S△BEC=6，
∴
BCEO=6，
即BC×OE=12=BO×AB=|k|．
∵反比例函数图象在第一象限，k＞0．
∴k=12．
故答案是：12．
练习册系列答案
相关题目
