Question

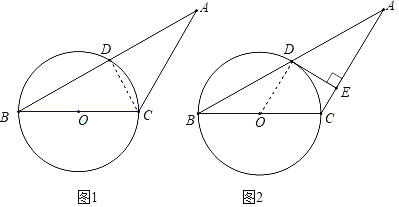
【题目】如图1，在△ABC中，AC＝BC，以BC为直径的⊙O交AB于点D．

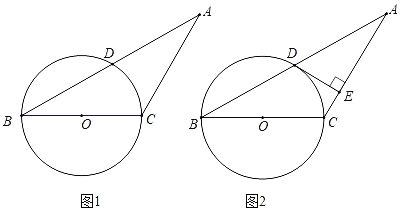
（1）求证：点D是AB的中点；

（2）如图2，过点D作DE⊥AC于点E，求证：DE是⊙O的切线．

Answer 1

【答案】（1）详见解析；（2）详见解析

【解析】

（1）由于AC＝AB，如果连接CD，那么只要证明出CD⊥AB，根据等腰三角形三线合一的特点，我们就可以得出AD＝BD，由于BC是圆的直径，那么CD⊥AB，由此可证得．

（2）连接OD，再证明OD⊥DE即可．

证明：（1）如图1，连接CD，

∵BC为⊙O的直径，

∴CD⊥AB．

∵AC＝BC，

∴AD＝BD．

（2）如图2，连接OD；

∵AD＝BD，OB＝OC，

∴OD是△BCA的中位线，

∴OD∥AC．

∵DE⊥AC，

∴DF⊥OD．

∵OD为半径，

∴DE是⊙O的切线．