Question

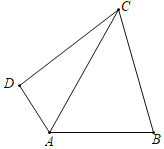
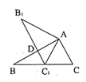
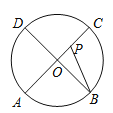
【题目】如图，M为线段AB的中点，AE与BD交于点C，，且DM交AC于F，ME交BC于点G．

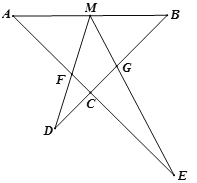
（1）写出图中相似三角形，并证明其中的一对；

（2）请连结FG，如果，，，求BG、FG的长．

Answer 1

【答案】（1）△AME∽△MFE，△BMD∽△MGD，△AMF∽△BGM，证明见解析；（2）BG＝，FG＝．

【解析】

（1）根据已知条件，∠DME＝∠A＝∠B＝，结合图形上的公共角，即可推出△DMG∽△DBM，△EMF∽△EAM，AMF∽△BGM；

（2）根据相似三角形的性质，推出BG的长度，依据锐角三角函数推出AC的长度，即可求出CG、CF的长度，继而推出FG的长度．

（1）△AME∽△MFE，△BMD∽△MGD，△AMF∽△BGM，

∵∠AMD＝∠B＋∠D，∠BGM＝∠DMG＋∠D

又∠B＝∠A＝∠DME＝

∴∠AMF＝∠BGM，

∴△AMF∽△BGM，

（2）当＝45°时，可得AC⊥BC且AC＝BC，

∵M为AB的中点，

∴AM＝BM＝2，

∵∠DME＝∠A＝∠B＝，∠FMB是△AFM的外角，

∴∠FMB＝∠A＋∠AFM＝∠DME＋∠GMB，

∴∠AFM＝∠GMB，

∴△AMF∽△BGM，

∴

∴BG＝＝＝，AC＝BC＝4cos45°＝4，

∴CG＝4＝，CF＝43＝1，

∴FG＝．