题目内容
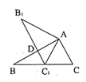
【题目】如图,将![]() 绕顶点A顺时针旋转
绕顶点A顺时针旋转![]() 后得到
后得到![]() ,且
,且![]() 为
为![]() 的中点,
的中点,![]() 与
与![]() 相交于
相交于![]() ,若
,若![]() ,则线段
,则线段![]() 的长度为________.
的长度为________.
【答案】![]()
【解析】
根据旋转的性质可知△ACC1为等边三角形,进而得出BC1=CC1=AC1=2,△ADC1是含30°的直角三角形,得到DC1的长,利用线段的和差即可得出结论.
根据旋转的性质可知:AC=AC1,∠CAC1=60°,B1C1=BC,∠B1C1A=∠C,
∴△ACC1为等边三角形,
∴∠AC1C=∠C=60°,CC1=AC1.
∵C1是BC的中点,
∴BC1=CC1=AC1=2,
∴∠B=∠C1AB=30°.
∵∠B1C1A=∠C=60°,
∴∠ADC1=180°-(∠C1AB+∠B1C1A)=180°-(30°+60°)=90°,
∴DC1=![]() AC1=1,
AC1=1,
∴B1D=B1C1-DC1=4-1=3.
故答案为:3.

练习册系列答案
相关题目