Question

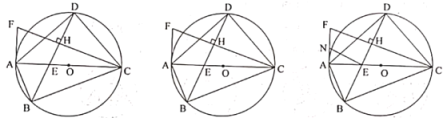
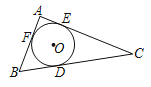
【题目】如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E．F．且AB＝5，AC＝12，BC＝13，则⊙O的半径是_____．

Answer 1

【答案】2

【解析】

由题意根据勾股定理的逆定理可得三角形ABC为直角三角形，再根据切线长定理即可求解．

解：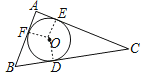

如图，连接OD、OE、OF，

∵△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E．F，

∴OE⊥AC，OF⊥AB，AE＝AF，

∵AB＝5，AC＝12，BC＝13，

即52+122＝132，

∴△ABC为直角三角形，

∴∠A＝90°，

∴四边形AEOF是正方形，

∴OE＝OF＝AE＝AF，

设⊙O的半径是r，

则AF＝AE＝r，BF＝BD＝5﹣r，EC＝DC＝12﹣r，

∵BD+DC＝BC＝13，

∴5﹣r+12﹣r＝13，

解得r＝2．

所以⊙O的半径是2．

故答案为2．