题目内容
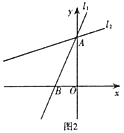
【题目】如图，直线
与
的图象交于点
，直线
与反比例函数
的图象交于
、
两点.
（1）直接写出
，
，
，
的值；
（2） 点
在平面内，若以
，
，
，四点为顶点的四边形是平行四边形，求符合条件的所有点的坐标.
【答案】（1）
； （2）
或
或P（0，5）
【解析】
（1）现将
代入
可得a的值以及A点的坐标，再将A点坐标代入
中，可得m的值，再将
、
代入
可得b、c的值
（2）根据平行四边形的性质对边平行可得出直线OP的解析式，再设
点坐标，根据平行四边形对变相等，列出方程即可求解
解：（1）将代入得：
∴A
将A代入中，可得：
，解得：
；
将代入得：
∴
将代入得：
∴
故答案为：；
（2）由题意，若以
，
，
，
四点为顶点的四边形是平行四边形，则可得
①当OP∥AB；
∴
，OP=AB；
∵OP过原点
∴OP的函数解析式为正比例函数
∴
设
又∵OP=AB，
∴
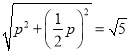
解得：p=2或p=﹣2
∴或
②当AB为对角线时，∵A（1，3），O（0，0），B（-1，2），
解得：
，
∴点P3的坐标为（0，5）；
∴综上所述：当以A，B，O，P四点为顶点的四边形是平行四边形时，P点的坐标为（-2，-1），（2，1）或（0，5）.
练习册系列答案
相关题目
