题目内容
如图,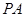 、
、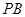 分别切⊙
分别切⊙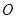 于点
于点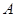 、
、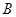 ,点
,点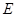 是⊙
是⊙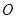 上一点,且
上一点,且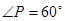 ,则
,则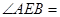 度;若PA=4,则AO= .
度;若PA=4,则AO= .
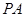 、
、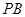 分别切⊙
分别切⊙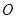 于点
于点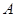 、
、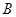 ,点
,点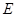 是⊙
是⊙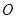 上一点,且
上一点,且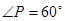 ,则
,则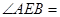 度;若PA=4,则AO= .
度;若PA=4,则AO= .
120;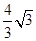 .
.
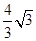 .
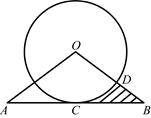
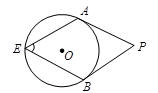
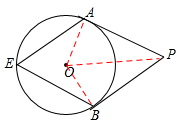
.试题分析:连接OA,BO,OP,由圆周角定理知可知∠AOB=2∠E,PA、PB分别切⊙O于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠AOB=180°-∠P=180°-60°=120°,从而得出∠AEB的度数;再由切线长定理得出∠APO=30°,根据三角函数求解即可:
如图,连接OA,BO,OP,
∵PA、PB分别切⊙O,∴∠OAP=∠OBP=90°.
∵∠P=60°,∴∠AOB=180°-∠P=180°-60°=120°.
∵∠AOB=2∠E=120°,∴∠AEB=60°.
∵∠P=60°,∴∠APO=30°.
∴Rt△AOP中,
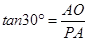 ,
,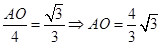 .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
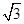 为半径作圆,点M(a,b) 是⊙P上的一点,设
为半径作圆,点M(a,b) 是⊙P上的一点,设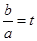 ,则
,则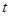 的取值范围是 .
的取值范围是 . 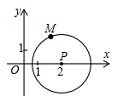

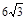 ,则图中阴影部分的面积为 (结果保留π).
,则图中阴影部分的面积为 (结果保留π).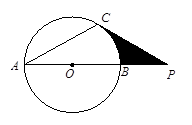
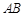 与⊙O相切于点
与⊙O相切于点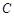 ,连结
,连结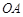 、
、 ,
,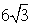 cm.
cm.