题目内容
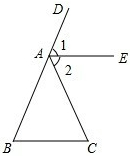如图，点D是△ABC的BA边的延长线上一点，有以下三项：AB=AC，∠1=∠2，AE∥BC，请把其中两项作为条件，填入下面的“已知”栏中，另一项作为结论，填入下面的“求证”栏中，使之组成一个真命题，并写出证明过程．已知：
AE∥BC，∠1=∠2
AE∥BC，∠1=∠2
，求证：
AB=AC
AB=AC
．证明：
分析：根据等腰三角形的判定定理可知，可把AE∥BC，∠1=∠2作为已知条件，AB=AC作为结论．先由AE∥BC得出∠1=∠B，∠2=∠C，再由∠1=∠2可知∠B=∠C，由等角对等边即可得出结论．
解答：已知：AE∥BC，∠1=∠2，
求证：AB=AC．
证明：∵AE∥BC，
∴∠1=∠B，∠2=∠C，
∵∠1=∠2，
∴∠B=∠C，
∴AB=AC．
故答案为：AE∥BC，∠1=∠2；AB=AC．
求证：AB=AC．
证明：∵AE∥BC，
∴∠1=∠B，∠2=∠C，
∵∠1=∠2，
∴∠B=∠C，
∴AB=AC．
故答案为：AE∥BC，∠1=∠2；AB=AC．
点评：本题考查的是等腰三角形的判定与性质，熟知等角对等边是解答此题的关键．
练习册系列答案
相关题目
如图，点F是△ABC外接圆
27、如图，点P是△ABC内的一点，有下列结论：①∠BPC＞∠A；②∠BPC一定是钝角；③∠BPC=∠A+∠ABP+∠ACP．其中正确的结论共有（ ）
如图，点O是△ABC内任意一点，G、D、E分别为AC、OA、OB的中点，F为BC上一动点，问四边形GDEF能否为平行四边形？若可以，指出F点位置，并给予证明．
（2013•攀枝花模拟）如图，点G是△ABC的重心，CG的延长线交AB于D，GA=5，GC=4，GB=3，将△ADG绕点D顺时针方向旋转180°得到△BDE，则△EBC的面积=
（1997•天津）如图，点I是△ABC的内心，AI交BC边于D，交△ABC的外接圆于点E．