题目内容
 (2013•攀枝花模拟)如图,点G是△ABC的重心,CG的延长线交AB于D,GA=5,GC=4,GB=3,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积=
(2013•攀枝花模拟)如图,点G是△ABC的重心,CG的延长线交AB于D,GA=5,GC=4,GB=3,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积=12
12
.分析:根据点G是△ABC的重心,CG的延长线交AB于D,GA=5,GC=4,GB=3,将△ADG绕点D顺时针方向旋转180°得到△BDE,得出DG=DE=2,以及BE=5,即可得出△EBG的面积,进而得出答案.
解答:解:∵点G是△ABC的重心,CG的延长线交AB于D,GC=4,
∴DE=2,
∵将△ADG绕点D顺时针方向旋转180°得到△BDE,
∴DG=DE=2,AG=BE=5,∵BG=3,
∴△BGE是直角三角形,
∴△BGE的面积为:
×3×4=6,
∵∠BGE=90°,
∴∠BGC=90°,
∴△BGC的面积为:
×3×4=6,
∴△EBC的面积为:12.
故答案为:12.
∴DE=2,
∵将△ADG绕点D顺时针方向旋转180°得到△BDE,
∴DG=DE=2,AG=BE=5,∵BG=3,
∴△BGE是直角三角形,
∴△BGE的面积为:
| 1 |
| 2 |
∵∠BGE=90°,
∴∠BGC=90°,
∴△BGC的面积为:
| 1 |
| 2 |
∴△EBC的面积为:12.
故答案为:12.
点评:此题主要考查了重心的性质以及勾股定理的应用,根据已知得出△BGE是直角三角形是解题关键.

练习册系列答案
相关题目

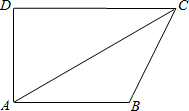 (2013•攀枝花模拟)在四边形ABCD中,AB∥CD,∠D=90°,∠DCA=30°,CA平分∠DCB,AD=4cm,
(2013•攀枝花模拟)在四边形ABCD中,AB∥CD,∠D=90°,∠DCA=30°,CA平分∠DCB,AD=4cm,