题目内容
【题目】如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE与CF相交于D,则:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上,正确的结论是( )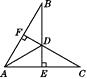
A.①②③
B.②③
C.①③
D.①
【答案】A
【解析】解 :∵BE⊥AC于E,CF⊥AB于F
∴∠AEB=∠AFC=90,
∵AB=AC,∠A=∠A,
∴△ABE≌△ACF,故①正确,
∴AE=AF,
∴BF=CE,
∵BE⊥AC于E,CF⊥AB于F,
∴∠BFD=∠CED=90°
又∵∠BDF=∠CDE,
∴△BDF≌△CDE 故②正确;
∴DF=DE,
∵AE=AF,DE=DF,AD=AD,
∴△AED≌△AFD,
∴∠FAD=∠EAD,
即点D在∠BAC的平分线上;故③正确;
故应选 :A ,
根据垂直的定义得出∠AEB=∠AFC=90,然后利用AAS判断出△ABE≌△ACF,根据全等三角形对应边相等得出AE=AF,进而得出BF=CE,根据垂直的定义得出∠BFD=∠CED=90°,进而利用AAS判断出△BDF≌△CDE,根据全等三角形对应边相等得出DF=DE,从而利用SSS判断出△AED≌△AFD,根据全等三角形对应角相等得出∠FAD=∠EAD,从而得出即点D在∠BAC的平分线上。

练习册系列答案
相关题目
【题目】在本学期某次考试中,某校初二(1)、初二(2)两班学生数学成绩统计如下表:、
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人 | 二(1)班 | 3 | 5 | 16 | 3 | 11 | 12 |
二(2)班 | 2 | 5 | 11 | 12 | 13 | 7 | |
请根据表格提供的信息回答下列问题:
(1)二(1)班平均成绩为分,二(2)班平均成绩为分,从平均成绩看两个班成绩优次?
(2)二(1)班众数为分,二(2)班众数为分.从众数看两个班的成绩谁优谁次? .
(3)已知二(1)班的方差大于二(2)班的方差,那么说明什么?


