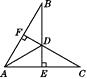
题目内容
【题目】如图,AB是⊙O的直径,⊙O交BC于D,过D作⊙O的切线DE交AC于E,且DE⊥AC,由上述条件,你能推出的正确结论有:_____________.
(要求:不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,至少写出4个结论,结论不能类同)

【答案】∠ADB=∠AED=∠CED=90°,△ADE∽△ABD,∠ADE=∠B,∠CAD=∠BAD,DE2=CE·EA,AD2=AE·AC=AE·AB,CD2=CE·CA,AB=AC,∠B=∠C,CD=BD,…
【解析】试题分析:由弦切角定理可证∠EDA=∠B,又已知DE⊥AC,则有∠EAD=∠B,即可证△ADE∽△ABD;又因为AB是直径,可证∠ADB=∠ADC=∠DEA=90°,利用相似的判定及性质可证出相应的乘积式.
解:由弦切角定理知,∠EDA=∠B,
∵DE⊥AC,AB是O的直径,
∴∠DEA=∠ADB=90°,
∵∠EDA=∠B,
∴△ADE∽△ABD;
∵AB是直径,
∴∠ADB=∠ADC=∠DEA=90°,
∠ADB=∠AED=∠CED=90°,
∵△ADE∽△ABD,
∴AD2=AE·AB
∴△ADE∽△ABD,∠ADE=∠B,∠CAD=∠BAD,AD2=AE·AB.

练习册系列答案
相关题目