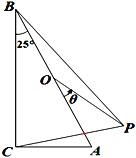
题目内容
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( ) 
A.∠BAC=70°
B.∠DOC=90°
C.∠BDC=35°
D.∠DAC=55°
【答案】B
【解析】解:∵∠ABC=50°,∠ACB=60°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣50°﹣60°=70°,
故A选项正确,
∵BD平分∠ABC,
∴∠ABO= ![]() ∠ABC=
∠ABC= ![]() ×50°=25°,
×50°=25°,
在△ABO中,
∠AOB=180°﹣∠BAC﹣∠ABO=180°﹣70°﹣25°=85°,
∴∠DOC=∠AOB=85°,
故B选项错误;
∵CD平分∠ACE,
∴∠ACD= ![]() (180°﹣60°)=60°,
(180°﹣60°)=60°,
∴∠BDC=180°﹣85°﹣60°=35°,
故C选项正确;
∵BD、CD分别是∠ABC和∠ACE的平分线,
∴AD是△ABC的外角平分线,
∴∠DAC= ![]() (180°﹣70°)=55°,
(180°﹣70°)=55°,
故D选项正确.
故选:B.
根据三角形的内角和定理列式计算即可求出∠BAC=70°,再根据角平分线的定义求出∠ABO,然后利用三角形的内角和定理求出∠AOB再根据对顶角相等可得∠DOC=∠AOB,根据邻补角的定义和角平分线的定义求出∠DCO,再利用三角形的内角和定理列式计算即可∠BDC,判断出AD为三角形的外角平分线,然后列式计算即可求出∠DAC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP= ![]() ,PD=
,PD= ![]() ,若
,若![]() 与
与![]() 之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
之间的函数关系的图象如图2所示,则等边△ABC的面积为( )

A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()