题目内容
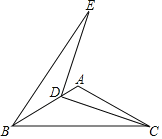
【题目】如图,在△ABC中,∠BAC=120°,AB=AC=6,D为边AB上一动点(不与B点重合),连接CD,将线段CD绕着点D逆时针旋转90°得到DE,连接BE,则S△BDE的最大值为_____.
【答案】![]()
【解析】
作CM⊥AB于M,EN⊥AB于N,根据AAS证得△EDN≌△DCM,得出EN=DM,然后解直角三角形求得AM=3,得到BM=9,设BD=x,则EN=DM=9-x,根据三角形面积公式得到S△BDE=![]() BDEN=
BDEN=![]() x(9-x)=-
x(9-x)=-![]() (x-4.5)2+
(x-4.5)2+![]() ,根据二次函数的性质即可求得.
,根据二次函数的性质即可求得.
作CM⊥AB于M,EN⊥AB于N,
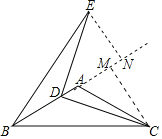
∴∠EDN+∠DEN=90°,
∵∠EDC=90°,
∴∠EDN+∠CDM=90°,
∴∠DEN=∠CDM,
在△EDN和△DCM中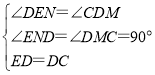 ,
,
∴△EDN≌△DCM(AAS),
∴EN=DM,
∵∠BAC=120°,
∴∠MAC=60°,
∴∠ACM=30°,
∴AM=![]() AC=
AC=![]() ×6=3,
×6=3,
∴BM=AB+AM=6+3=9,
设BD=x,则EN=DM=9-x,
∴S△BDE=![]() BDEN=
BDEN=![]() x(9-x)=-
x(9-x)=-![]() (x-4.5)2+
(x-4.5)2+![]() ,
,
∴当BD=4.5时,S△BDE有最大值为![]() ,
,
故答案为![]() .
.

【题目】某校在“校园体育文化节”活动中组织了“球类知识我知道”的竞赛活动,从初三年级1200名学生中随机抽查了100名学生的成绩(满分30分),整理得到如下的统计图表:
成绩(分) | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
频率统计表
成绩分组 | 频数 | 频率 |
15≤x<18 | 3 | 0.03 |
18≤x<21 | a | 0.12 |
21≤x<24 | 20 | 0.20 |
24≤x<27 | 35 | 0.35 |
27≤x≤30 | 30 | b |
频数分布直方图
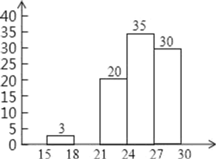
请根据所提供的信息解答下列问题:
(1)样本的众数是 分,中位数是 分;
(2)频率统计表中a= ,b= ;补全频数分布直方图;
(3)请根据抽样统计结果,估计该次竞赛中初三年级成绩不少于21分的大约有多少人?随机抽取一名同学的成绩,其值不小于24分的概率是多少?