��Ŀ����
����Ŀ����ͼ��������y��ax2+bx+3��a��0����x�ᣬy��ֱ��ڵ�A����1��0����B��3��0������C���㣮
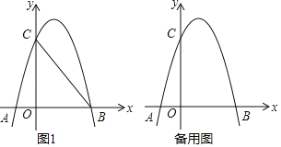
��1�����������ߵĽ���ʽ��
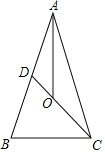
��2����D��2��m���ڵ�һ�����������ϣ�����BC��BD�����ʣ��ڶԳ����������������Ƿ����һ��P�������PBC����DBC��������ڣ��������P������ꣻ��������ڣ���˵�����ɣ�
��3����N�������ߵĶԳ����ϣ���M���������ϣ�����M��N��B��CΪ������ı�����ƽ���ı���ʱ����ֱ��д����M�����꣮
���𰸡���1��y����x2+2x+3����2�����ڣ����ɼ���������3��M1����2����5����M2��4����5����M3��2��3����
��������
��1������֪��Ӧ�ô���ϵ��������ɽ⣻
��2��������֪���������D�����꣬�������߶�OC��OB��ȡ�CD��x�ἰ��������������֤����CDB�ա�CGB������ȫ�������������G�����꣬���ֱ��BP�Ľ���ʽ���������κ�������ʽ�������P�����꣮
��3�������N���꣬����ƽ���ı��ζԽ�����ƽ�ֵ����ʣ���ʾ��M���꣬���뺯����ϵʽ������ɽ�.
�⣺��ͼ��
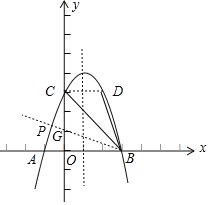
��1����������y��ax2+bx+3��a��0����x�ᣬy��ֱ��ڵ�A����1��0����B��3��0������C���㣮
��![]() ���
���![]()
�������ߵĽ���ʽΪy����x2+2x+3��
��2�����ڣ��������£�
y����x2+2x+3������x��1��2+4��
�ߵ�D��2��m���ڵ�һ�����������ϣ�
��m��3����D��2��3����
��C��0��3��
��OC��OB��
���OBC����OCB��45����
����CD����CD��x�ᣬ
���DCB����OBC��45����
���DCB����OCB��
��y����ȡ��G��ʹCG��CD��2��
���ӳ�BG���������ڵ�P��
����DCB����GCB��
CB��CB����DCB����OCB��CG��CD��
���DCB�ա�GCB��SAS��
���DBC����GBC��
��ֱ��BP����ʽΪyBP��kx+b��k��0������G��0��1����B��3��0�����룬��
k����![]() ��b��1��
��b��1��
��BP����ʽΪyBP����![]() x+1��
x+1��
yBP����![]() x+1��y����x2+2x+3
x+1��y����x2+2x+3
��y��yBP ʱ����![]() x+1����x2+2x+3��
x+1����x2+2x+3��
���x1����![]() ��x2��3����ȥ����
��x2��3����ȥ����
��y��![]() ��
��
��P����![]() ��
��![]() ����
����
��3��M1����2����5����M2��4����5����M3��2��3����
���N������1span>��n��
��BC��MNΪƽ���ı��ζԽ���ʱ����BC��MN����ƽ�֣�M����Ϊ��2,3-n��
����y����x2+2x+3��3-n=��22+4+3��n=0��M��2,3��
��BM��NCΪƽ���ı��ζԽ���ʱ����BM��NC����ƽ�֣�M����Ϊ��-2,3+n��
����y����x2+2x+3��3+n=��4-4+3��n=-8��M��-2,-5��
��MC��BNΪƽ���ı��ζԽ���ʱ����MC��BN����ƽ�֣�M����Ϊ��4, n-3��
����y����x2+2x+3��n-3=��16+8+3��n=-2��M��4,-5��
�ʴ�Ϊ��M1����2����5����M2��4����5����M3��2��3��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�