题目内容
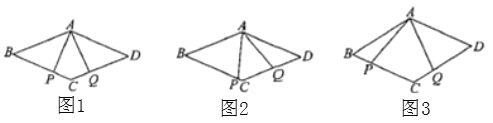
【题目】已知点![]() 分别在菱形
分别在菱形![]() 的边
的边![]() 上滑动(点
上滑动(点![]() 不与
不与![]() 重合),且
重合),且![]() .
.
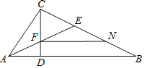
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 与
与![]() 不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
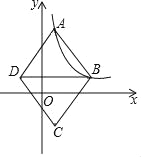
(3)如图3,若![]() ,请直接写出四边形
,请直接写出四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)(1)中的结论还成立,证明见解析;(3)四边形![]() 的面积为
的面积为![]() .
.
【解析】
(1)根据菱形的性质及已知,得到![]() ,再证
,再证![]() ,
,
根据三角形全等的性质即可得到结论;
(2)作![]() ,垂足分别为点
,垂足分别为点![]() ,证明
,证明![]() ,根据三角形全等的性质即可得到结论;
,根据三角形全等的性质即可得到结论;
(3)根据菱形的面积公式,结合(2)的结论解答.
解:(1)∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
在![]() 和
和![]() 中,
中,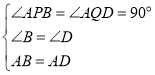 ,
,
∴![]() ,
,
∴![]() .
.
(2)若![]() 与
与![]() 不垂直,(1)中的结论还成立证明如下:
不垂直,(1)中的结论还成立证明如下:
如图,作![]() ,垂足分别为点
,垂足分别为点![]() .
.
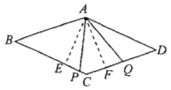
由(1)可得![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,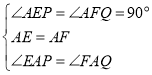 ,
,
∴![]() ,∴
,∴![]() .
.
(3)如图,连接![]() 交于点
交于点![]() .
.
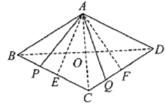
∵![]() ,∴
,∴![]() 为等边三角形,
为等边三角形,
∵![]() ,∴
,∴![]() ,同理,
,同理,![]() ,
,
∴四边形![]() 的面积
的面积![]() 四边形
四边形![]() 的面积,
的面积,
由(2)得四边形![]() 的面积
的面积![]() 四边形AECF的面积
四边形AECF的面积
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 的面积为
的面积为![]() ,
,
∴四边形![]() 的面积为
的面积为![]() .
.

练习册系列答案
相关题目
【题目】某商家计划从厂家采购空调和冰箱两种产品共![]() 台,空调和冰箱的采购单价与销售单价如表所示:
台,空调和冰箱的采购单价与销售单价如表所示:
采购单价 | 销售单价 | |
空调 |
|
|
冰箱 |
|
|
![]() 若采购空调
若采购空调![]() 台,且所采购的空调和冰箱全部售完,求商家的利润;
台,且所采购的空调和冰箱全部售完,求商家的利润;
![]() 厂家有规定,采购空调的数量不少于
厂家有规定,采购空调的数量不少于![]() 台,且空调采购单价不低于
台,且空调采购单价不低于![]() 元,问商家采购空调多少台时总利润最大?并求最大利润.
元,问商家采购空调多少台时总利润最大?并求最大利润.