题目内容
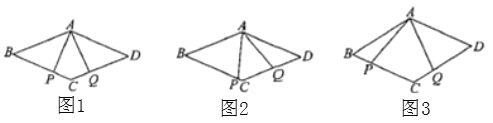
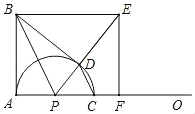
【题目】如图,∠BAO=90°,AB=8,动点P在射线AO上,以PA为半径的半圆P交射线AO于另一点C,CD∥BP交半圆P于另一点D,BE∥AO交射线PD于点E,EF⊥AO于点F,连接BD,设AP=m.
(1)求证:∠BDP=90°.
(2)若m=4,求BE的长.
(3)在点P的整个运动过程中.
①当AF=3CF时,求出所有符合条件的m的值.
②当tan∠DBE=![]() 时,直接写出△CDP与△BDP面积比.
时,直接写出△CDP与△BDP面积比.
【答案】(1)详见解析;(2)![]() 的长为10;(3)m的值为
的长为10;(3)m的值为![]() 或
或![]() ;
;![]() 与
与![]() 面积比为
面积比为![]() 或
或![]() .
.
【解析】
![]() 由
由![]() 知
知![]() ,再由
,再由![]() 知
知![]() 、
、![]() ,据此可得
,据此可得![]() ,证
,证![]() ≌
≌![]() 即可得;
即可得;![]() 易知四边形ABEF是矩形,设
易知四边形ABEF是矩形,设![]() ,可得
,可得![]() ,证
,证![]() ≌
≌![]() 得
得![]() ,在
,在![]() 中,由
中,由![]() ,列方程求解可得答案;
,列方程求解可得答案;![]() 分点C在AF的左侧和右侧两种情况求解:左侧时由
分点C在AF的左侧和右侧两种情况求解:左侧时由![]() 知
知![]() 、
、![]() 、
、![]() ,在
,在![]() 中,由
中,由![]() 可得关于m的方程,解之可得;右侧时,由
可得关于m的方程,解之可得;右侧时,由![]() 知
知![]() 、
、![]() 、
、![]() ,利用勾股定理求解可得.
,利用勾股定理求解可得.![]() 作
作![]() 于点G,延长GD交BE于点H,由
于点G,延长GD交BE于点H,由![]() ≌
≌![]() 知
知![]() ,据此可得
,据此可得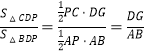 ,再分点D在矩形内部和外部的情况求解可得.
,再分点D在矩形内部和外部的情况求解可得.
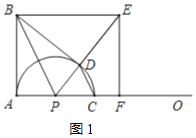
![]() 如图1,
如图1,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形ABEF是矩形,
四边形ABEF是矩形,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,
,
![]() 的长为10.
的长为10.
![]() 如图1,当点C在AF的左侧时,
如图1,当点C在AF的左侧时,
![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() 负值舍去
负值舍去![]() ;
;
如图2,当点C在AF的右侧时,
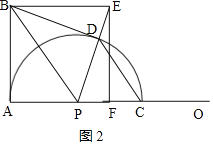
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() 负值舍去
负值舍去![]() ;
;
综上,m的值为![]() 或
或![]() ;
;
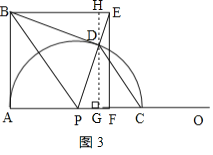
![]() 如图3,过点D作
如图3,过点D作![]() 于点G,延长GD交BE于点H,
于点G,延长GD交BE于点H,
![]() ≌
≌![]() ,
,
![]() ,
,
又![]() ,且
,且![]() ,
,
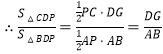 ,
,
当点D在矩形ABEF的内部时,
由![]() 可设
可设![]() 、
、![]() ,
,
则![]() ,
,
![]() ,
,
则![]() ;
;
如图4,当点D在矩形ABEF的外部时,

由![]() 可设
可设![]() 、
、![]() ,
,
则![]() ,
,
![]() ,
,
则![]() ,
,
综上,![]() 与
与![]() 面积比为
面积比为![]() 或
或![]() .
.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目