题目内容
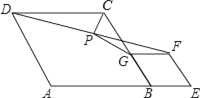
【题目】如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC＝∠BEF＝60°，则
＝_____．
【答案】
【解析】
延长GP交CD于M，如图，根据菱形的性质得GF∥CD，∠BCD=120°，CD=CB，GB=GF，则利用平行线的性质得∠PDM=∠PFG，于是可判断△PDM≌△PFG，所以MD=GF，PM=PG，接着证明CM=CG，则根据等腰三角形的性质有CP⊥MG，CP平分∠MCG，所以∠PGC=30°，然后根据含30度的直角三角形三边的关系求解．
延长GP交CD于M，如图，
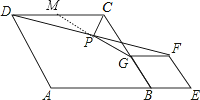
∵四边形ABCD和BEFG为菱形，点A、B、E在同一直线上，
∴GF∥CD，∠BCD=120°，CD=CB，GB=GF，
∴∠PDM=∠PFG，
在△PDM和△PFG中，
，
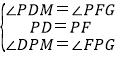∴△PDM≌△PFG，
∴MD=GF，PM=PG，
∴MD=GB，
∴CM=CG，
∵PM=PG，
∴CP⊥MG，CP平分∠MCG，
∴∠PCG=60°，
∴∠PGC=30°，
∴
．
故答案为．
练习册系列答案
相关题目
